
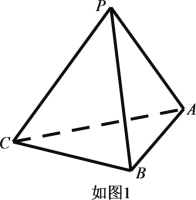
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的正切值.
的正切值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() (2)由
(2)由![]() ,得
,得![]() 平面
平面![]() ,从而
,从而![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,且
所成角,且![]() ,进而当
,进而当![]() 最短时,即
最短时,即![]() 是
是![]() 中点时,
中点时,![]() 最大,由
最大,由![]() 平面
平面![]() ,得
,得![]() ,以
,以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,利用向量法先求出二面角的余弦值,根据同角三角函数关系即可求出正切值.
轴,建立空间直角坐标系,利用向量法先求出二面角的余弦值,根据同角三角函数关系即可求出正切值.
(1 )三棱锥![]() (如图1)的平面展开图(如图2)中
(如图1)的平面展开图(如图2)中
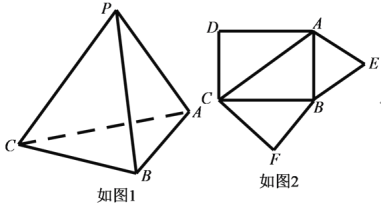
四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,
均为正三角形,
![]()
![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() ,
,
则![]() ,
,
且![]() ,
,
![]()
![]() ,
,
又![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]()
(2)由(1)知![]() ,
,
![]() ,
,
![]() 平面
平面![]()
![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,且
所成角,且![]() ,
,
![]() 当
当![]() 最短时,即
最短时,即![]() 是
是![]() 中点时,
中点时,![]() 最大,
最大,
由![]() 平面
平面![]() ,得
,得![]() ,
,
![]() 以
以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,如图:
轴,建立空间直角坐标系,如图:
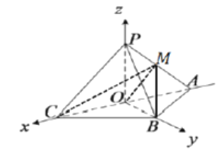
则![]() ,
,
![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则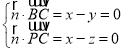 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
所以![]() ,
,
![]() 二面角
二面角![]() 的正切值为
的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校高一、高二、高三三个年级共有![]() 名教师,为调查他们的备课时间情况,通过分层抽样获得了
名教师,为调查他们的备课时间情况,通过分层抽样获得了![]() 名教师一周的备课时间,数据如下表(单位:小时).
名教师一周的备课时间,数据如下表(单位:小时).
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(1)试估计该校高三年级的教师人数;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲,高二年级选出的人记为乙,求该周甲的备课时间不比乙的备课时间长的概率;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是![]() ,
, ![]() ,
, ![]() (单位:小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位:小时),这三个数据与表格中的数据构成的新样本的平均数记为![]() ,表格中的数据平均数记为
,表格中的数据平均数记为![]() ,试判断
,试判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)可近似看作一次函数
(元/件)可近似看作一次函数![]() 的关系(如图所示).
的关系(如图所示).

(1)由图象,求函数![]() 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价﹣成本总价)为![]() 元.试用销售单价
元.试用销售单价![]() 表示毛利润
表示毛利润![]() ,并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
,并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市政府为了促进低碳环保的出行方式,从全市在册的50000辆电动车中随机抽取100辆,委托专业机构免费为它们进行电池性能检测.电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如下图.
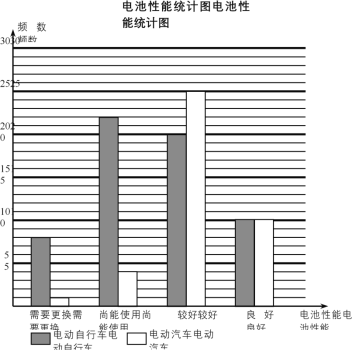
(1)从电池性能较好的电动车中,采用分层抽样的方法随机抽取了9辆,求再从这9辆电动车中随机抽取2辆,至少有1辆为电动汽车的概率;
(2)为提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:
①电动自行车每辆补助300元;
②电动汽车每辆补助500元;
③对电池需要更换的电动车每辆额外补助400元.
利用样本估计总体,试估计市政府执行此方案的预算(单位:万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国已经成为全球最大的电商市场,但是实体店仍然是消费者接触商品和品牌的重要渠道.某机构随机抽取了年龄介于10岁到60岁的消费者200人,对他们的主要购物方式进行问卷调查.现对调查对象的年龄分布及主要购物方式进行统计,得到如下图表:
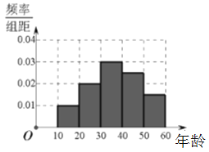
主要购物方式 年龄阶段 | 网络平台购物 | 实体店购物 | 总计 |
40岁以下 | 75 | ||
40岁或40岁以上 | 55 | ||
总计 |
(1)根据已知条件完成上述列联表,并据此资料,能否在犯错误的概率不超过![]() 的前提下,认为消费者主要的购物方式与年龄有关?
的前提下,认为消费者主要的购物方式与年龄有关?
(2)用分层抽样的方法从通过网络平台购物的消费者中随机抽取8人,然后再从这8名消费者中抽取5名进行答谢.设抽到的消费者中40岁以下的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: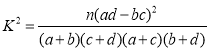 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题是全称量词命题还是存在量词命题.
(1)梯形的对角线相等;
(2)存在一个四边形有外接圆
(3)二次函数的图象都与x轴相交;
(4)存在一对实数x,y,使![]() 成立
成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题是否正确,正确的说明理由,错误的举例说明.
(1)一条直线平行于一个平面,另一条直线与这个平面垂直,则这两条直线互相垂直;
(2)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 与平面
与平面![]() 所成的二面角和平面
所成的二面角和平面![]() 与平面
与平面![]() 所成的二面角相等或互补;
所成的二面角相等或互补;
(3)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.
(单位:亿元)的折线图.
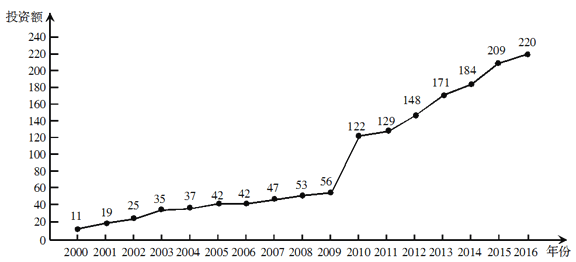
为了预测该地区2018年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型①:
)建立模型①:![]() ;根据2010年至2016年的数据(时间变量
;根据2010年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型②:
)建立模型②:![]() .
.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月27日当今世界围棋排名第一的柯洁在与![]() 的人机大战中中盘弃子认输,至此柯洁与
的人机大战中中盘弃子认输,至此柯洁与![]() 的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

(1)请根据已知条件完成下面![]() 列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)为了进一步了解“围棋迷”的围棋水平,从“围棋迷”中按性别分层抽样抽取5名学生组队参加校际交流赛,首轮该校需派两名学生出赛,若从5名学生中随机抽取2人出赛,求2人恰好一男一女的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com