练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    方程的曲线即为函数的图象，对于函数，下列命题中正确的是 .（请写出所有正确命题的序号）

    ①函数在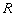上是单调递减函数； ②函数的值域是；

    ③函数的图象不经过第一象限； ④函数的图象关于直线对称；

    ⑤函数至少存在一个零点.

     

    【答案】

    ①②③

    【解析】

    试卷分析：对于①，当x≥0且y≥0时，方程为，此时方程不成立．

    当x＜0且y＜0时，方程为，此时．

    当x≥0且y＜0时，方程为，此时．

    当x＜0且y≥0时，方程为，此时．

    因此作出函数的大致图象，如下图所示

    由图象可知函数在R上单调递减，所以①成立．

    对于②，根据①所作的图象可知函数的值域为R，所以②正确．

    对于③，根据①所作的图象可知函数的图象不经过第一象限，所以③正确；

    对于④，根据①所作的图象可知函数的图象不关于直线对称；所以④错误；

    对于⑤由得．因为双曲线和

    的渐近线为，所以函数与直线至多有一个公共点，因此函数至多存在一个零点，可得⑤错误．

    考点：1.函数的性质及应用；2.圆锥曲线的定义、性质与方程；3.命题的真假判断与应用.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    方程
    x|x|
    16
    +
    y|y|
    9
    =-1的曲线即为函数y=f（x）的图象，对于函数y=f（x），有如下结论：
    ①f（x）在R上单调递减；
    ②函数F（x）=4f（x）+3x不存在零点；
    ③函数y=f（x）的值域是R；
    ④若函数g（x）和f（x）的图象关于原点对称，则函数y=g（x）的图象就是方程
    y|y|
    16
    +
    x|x|
    9
    =1确定的曲线．
    其中所有正确的命题序号是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•茂名二模）方程
    x|x|
    16
    +
    y|y|
    9
    =-1的曲线即为函数y=f（x）的图象，对于函数y=f（x），有如下结论：
    ①f（x）在R上单调递减；
    ②函数F（x）=4f（x）+3x不存在零点；
    ③函数y=f（x）的值域是R；
    ④f（x）的图象不经过第一象限，
    其中正确的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省烟台市高三（上）期末数学试卷（理科）（解析版） 题型：选择题

    方程+=-1的曲线即为函数y=f（x）的图象，对于函数y=f（x），有如下结论：
    ①f（x）在R上单调递减；
    ②函数F（x）=4f（x）+3x不存在零点；
    ③函数y=f（x）的值域是R；
    ④若函数g（x）和f（x）的图象关于原点对称，则函数y=g（x）的图象就是方程+=1确定的曲线．
    其中所有正确的命题序号是（ ）
    A．①②
    B．②③
    C．①③④
    D．①②③

    查看答案和解析>>

    科目：高中数学 来源：《圆锥曲线》2013年广东省十二大市高三二模数学试卷汇编（理科）（解析版） 题型：选择题

    方程+=-1的曲线即为函数y=f（x）的图象，对于函数y=f（x），有如下结论：
    ①f（x）在R上单调递减；
    ②函数F（x）=4f（x）+3x不存在零点；
    ③函数y=f（x）的值域是R；
    ④f（x）的图象不经过第一象限，
    其中正确的个数是（ ）
    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>

    同步练习册答案