已知数列
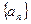
和
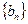
满足:
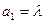
,
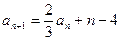
,
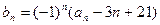
,
其中
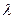
为实数,
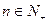
.
⑴ 对任意实数
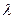
,证明数列
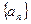
不是等比数列;
⑵ 证明:当
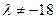
,数列
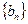
是等比数列;
⑶设
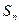
为数列
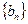
的前
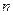
项和,是否存在实数
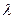
,使得对任意正整数
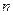
,都有
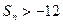
?
若存在,求
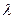
的取值范围;若不存在,说明理由.
⑴证明略⑵证明略⑶存在实数
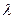
,使得对任意正整数
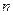
,都有
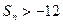
,
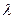
的取值范围为
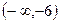
.
⑴证明:假设存在一个实数
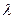
,使
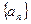
是等比数列,则有
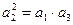
,
即
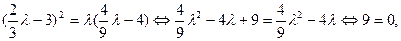
矛盾.
所以
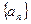
不是等比数列.
⑵ 解:因为
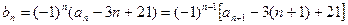
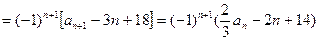
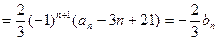
又
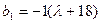
,所以,当
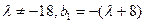
时,
由上可知
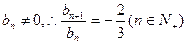
,
此时
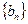
是以
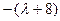
为首项,
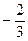
为公比的等比数列.
⑶当
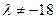
时,由⑵得
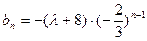
,于是
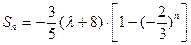
,
当
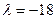
时,
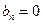
,从而
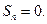
上式仍成立.要使对任意正整数n , 都有
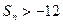
.即
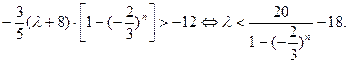
令
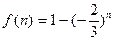
,则
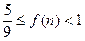
当n为正奇数时,
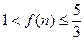
;当n为正偶数时,
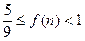
.
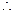
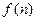
的最大值为
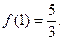
于是可得
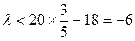
.
综上所述,存在实数
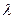
,使得对任意正整数
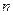
,都有
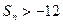
,
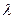
的取值范围为
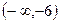
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
数列{a
n}的前n项和为S
n,且S
n=

(a
n-1).
(1)求a
1,a
2;
(2)证明:数列{a
n}是等比数列;
(3)求a
n及S
n.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知数列
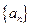
的前
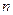
项和为
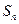
,且
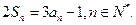
1)求数列
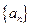
的通项公式;
2)求数列
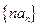
的前
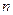
项和为
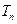
.
查看答案和解析>>

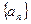 和
和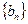 满足:
满足: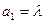 ,
,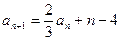 ,
,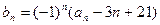 ,
,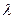 为实数,
为实数,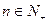 .
.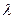 ,证明数列
,证明数列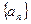 不是等比数列;
不是等比数列;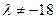 ,数列
,数列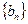 是等比数列;
是等比数列; 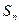 为数列
为数列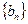 的前
的前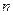 项和,是否存在实数
项和,是否存在实数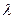 ,使得对任意正整数
,使得对任意正整数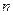 ,都有
,都有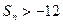 ?
?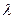 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. 53随堂测系列答案
53随堂测系列答案