
【题目】三棱锥P﹣ABC,底面ABC为边长为2 ![]() 的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为AP上一点,AD=2DP,O为底面三角形中心.
的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为AP上一点,AD=2DP,O为底面三角形中心. 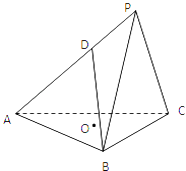
(1)求证DO∥面PBC;
(2)求证:BD⊥AC;
(3)设M为PC中点,求平面MBD和平面BDO所成锐二面角的余弦值.
【答案】
(1)证明:连接AO交BC于点E,连接PE.
∵O为正三角形ABC的中心,∴AO=2OE,
且E为BC中点.又AD=2DP,
∴DO∥PE,
∵DO平面PBC,PE平面PBC
∴DO∥面PBC.
(2)证明:∵PB=PC,且E为BC中点,∴PE⊥BC,
又平面PBC⊥平面ABC,
∴PE⊥平面ABC,
由(Ⅰ)知,DO∥PE,
∴DO⊥平面ABC,
∴DO⊥AC
连接BO,则AC⊥BO,又DO∩BO=O,
∴AC⊥平面DOB,∴AC⊥BD.
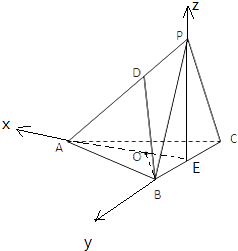
(3)解:由(1)(2)知,EA,EB,EP两两互相垂直,且E为BC中点,
所以分别以EA,EB,EP所在直线为x,y,z轴,建立空间直角坐标系,
如图,则A(3,0,0),B(0, ![]() ,0),P(0,0,1),
,0),P(0,0,1),
D(1,0, ![]() ),C(0,﹣
),C(0,﹣ ![]() ,0),M(0,﹣
,0),M(0,﹣ ![]() ,
, ![]() ),
),
∴ ![]() =(0,﹣
=(0,﹣ ![]() ,
, ![]() ),
), ![]() =(﹣1,
=(﹣1, ![]() ,﹣
,﹣ ![]() ),
),
设平面BDM的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 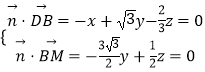 ,
,
令y=1,则 ![]() =(﹣
=(﹣ ![]() ,1,3
,1,3 ![]() ),
),
由(Ⅱ)知AC⊥平面DBO,
∴ ![]() =(﹣3,﹣
=(﹣3,﹣ ![]() ,0)为平面DBO的法向量,
,0)为平面DBO的法向量,
∴cos< ![]() >=
>= 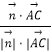 =
= ![]() =
= ![]() ,
,
由图可知,二面角M﹣BD﹣O的余弦值为 ![]() .
.
【解析】(1)连接AO交BC于点E,连接PE,推导出DO∥PE,由此能证明DO∥面PBC.(2)推导出PE⊥BC,从而PE⊥平面ABC,进而DO⊥平面ABC,由此得DO⊥AC,再由AC⊥BO,能证明AC⊥BD.(3)分别以EA,EB,EP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角M﹣BD﹣O的余弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点,以及对直线与平面平行的判定的理解,了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价﹣供货价格) 
(1)求售价15元时的销量及此时的供货价格;
(2)当销售价格为多少时总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点. 
(1)求证:AF⊥EF;
(2)求二面角A﹣PC﹣B的平面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2 的正方体ABCD﹣A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )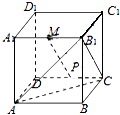
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,其中0<ω<2; (Ⅰ)若f(x)的最小正周期为π,求f(x)的单调增区间;
,其中0<ω<2; (Ⅰ)若f(x)的最小正周期为π,求f(x)的单调增区间;
(Ⅱ)若函数f(x)的图象的一条对称轴为 ![]() ,求ω的值.
,求ω的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点M(﹣2,0)的直线l与椭圆x2+2y2=2交于P1 , P2 , 线段P1P2的中点为P.设直线l的斜率为k1(k1≠0),直线OP的斜率为k2 , 则k1k2等于( )
A.﹣2
B.2
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx图象与直线x﹣y﹣4=0相切于(1,f(1))
(1)求实数a,b的值;
(2)若方程f(x)=m﹣7x有三个解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx在x=1处取得极值2.
(1)求f(x)的解析式;
(2)若(m+3)x﹣x2ex+2x2≤f(x)对于任意的x∈(0,+∞)成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com