练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    f(x)是一次函数，且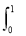f(x)dx＝5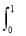，xf(x)dx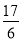＝，那么f(x)的解析式是________．

     

    f(x)＝4x＋3

    【解析】设f(x)＝ax＋b(a≠0)，则

    (ax＋b)dx＝axdx＋bdx＝ ax2|＋bx|＝ a＋b＝5.①

    x(ax＋b)dx＝(ax2＋bx)dx＝ax3|＋ bx2|＝a＋ b＝.②

    由①②解得a＝4，b＝3.故f(x)＝4x＋3.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标5章末练习卷（解析版） 题型：解答题

    已知x、y为共轭复数，且(x＋y)2－3xyi＝4－6i，求x、y.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标5.2习卷（解析版） 题型：选择题

    复数(3m－2)＋(m－1)i是虚数，则m满足 (　　)．

    A．m≠1 B．m≠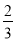

    C．m＝1 D．m＝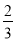

     

    查看答案和解析>>

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标4章末练习卷（解析版） 题型：选择题

    曲线y＝e－2x＋1在点(0,2)处的切线与直线y＝0和y＝x围成的

    三角形的面积为 ( )．

    A. B. C. D．1

     

    查看答案和解析>>

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标4章末练习卷（解析版） 题型：选择题

    曲线y＝－x3＋3x2在点(1,2)处的切线方程为 ( )．

    A．y＝3x－1 B．y＝－3x＋5

    C．y＝3x＋5 D．y＝2x

     

    查看答案和解析>>

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标4.5练习卷（解析版） 题型：解答题

    有一质量非均匀分布的细棒，已知其线密度为ρ(x)＝2x(取细棒所在直

    线为x轴，细棒的一端为原点)，棒长为l，试用定积分表示细棒的质量m，并求出m的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标4.4练习卷（解析版） 题型：解答题

    某企业拟建造如图所示的容器(不计厚度，长度单位：米)，其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的容积为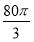立方米，且l≥2r.假设该容器的建造费用仅与其表面积有关，已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为c(c>3)千元．设该容器的建造费用为y千元．

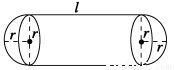
    ①写出y关于r的函数表达式，并求该函数的定义域；

    ②求该容器的建造费用最小时的r.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标4.3练习卷（解析版） 题型：解答题

    已知函数f(x)＝x3－ax－1

    (1)若f(x)在实数集R上单调递增，求a的取值范围；

    (2)是否存在实数a，使f(x)在(－1,1)上单调递减，若存在，求出a的取值范围；若不存在，说明理由；

    (3)证明f(x)＝x3－ax－1的图象不可能总在直线y＝a的上方．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届湘教版高二数学选修2-2基础达标4.2练习卷（解析版） 题型：解答题

    已知直线y＝kx是曲线y＝ln x的切线，求k.

     

    查看答案和解析>>

    同步练习册答案