Question

【题目】某公司近年来科研费用支出万元与公司所获利润万元之间有如表的统计

数据：参考公式：用最小二乘法求出关于的线性回归方程为： ，

其中： ， ，参考数值： 。

（Ⅰ）求出；

（Ⅱ）根据上表提供的数据可知公司所获利润万元与科研费用支出万元线性相关，请用最小二乘法求出关于的线性回归方程；

（Ⅲ）试根据（Ⅱ）求出的线性回归方程，预测该公司科研费用支出为10万元时公司所获得的利润。

Answer 1

【答案】（1）3.5，28（2）（3）64.4万元

【解析】试题分析：（1）利用平均值公式与所给参考数值求解即可；（2）利用公式求得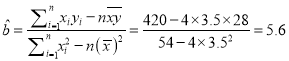，将样本中心点的坐标代入回归方程，求得，从而可得结果；（3）利用第二问的回归方程进行求值，预测即可

试题解析：（1）。

(2) ，

，

。

，

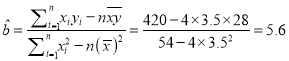所以回归方程为。

(3)当时， （万元），

故预测该公司科研费用支出为10万元时公司所获得的利润为64.4万元。

【方法点晴】本题主要考查线性回归方程，属于难题.求回归直线方程的步骤：①依据样本数据画出散点图，确定两个变量具有线性相关关系；②计算的值；③计算回归系数；④写出回归直线方程为； 回归直线过样本点中心是一条重要性质，利用线性回归方程可以估计总体，帮助我们分析两个变量的变化趋势.