
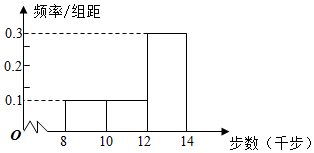
 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
分析 (1)由已知条件可估计中位数为12+$\frac{1}{6}×2$≈12.3,利用平均数公式能求出王师傅每天“健步走”的步数的平均数.
(2)利用对立事件的概率公式,即可求这2天的“健步走”结果不属于同一评价级别的概率.
解答 解:(1)由频率分布直方图,可估计中位数为12+$\frac{1}{6}×2$≈12.3(千步),
平均数为0.2×9+0.2×11+0.6×13=11.8(千步);
(2)设“在10天是任取2天,评价级别相同”为事件A,“在10天中任取2天,评价级别不相同”为事件B.
则$P(A)=\frac{C_2^2+C_2^2+C_6^2}{{C_{10}^2}}=\frac{17}{45}$.
∵事件A与事件B互为对立事件,
∴$P(B)=1-P(A)=1-\frac{17}{45}=\frac{28}{45}$.
点评 本题考查中位数及平均数的求法,考查概率的计算,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(-1,$\frac{1}{3}$).过椭圆E内一点P(1,$\frac{1}{2}$)的两条直线分别与椭圆交于点A、C和B、D,且满足$\overrightarrow{AP}$=λ$\overrightarrow{PC}$,$\overrightarrow{BP}$=λ$\overrightarrow{PD}$,其中λ为实数.当直线AP平行于x轴时,对应的λ=$\frac{1}{5}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(-1,$\frac{1}{3}$).过椭圆E内一点P(1,$\frac{1}{2}$)的两条直线分别与椭圆交于点A、C和B、D,且满足$\overrightarrow{AP}$=λ$\overrightarrow{PC}$,$\overrightarrow{BP}$=λ$\overrightarrow{PD}$,其中λ为实数.当直线AP平行于x轴时,对应的λ=$\frac{1}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )
如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )| A. | 28π | B. | 32π | C. | 16π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
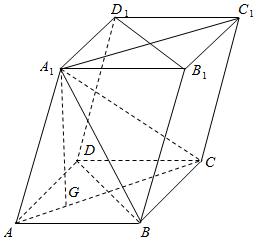 如图,在斜四棱柱ABCD-A1B1C1D1的底面是边长为2$\sqrt{3}$的菱形,且∠BAD=$\frac{π}{3}$,若∠AA1C=$\frac{π}{2}$,且A1在底面ABCD上的射影为△ABD的重心G.
如图,在斜四棱柱ABCD-A1B1C1D1的底面是边长为2$\sqrt{3}$的菱形,且∠BAD=$\frac{π}{3}$,若∠AA1C=$\frac{π}{2}$,且A1在底面ABCD上的射影为△ABD的重心G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有1个黑球和都是红球 | B. | 至少有1个黑球和都是黑球 | ||
| C. | 至少有1个黑球与至少1个红球 | D. | 恰有1个黑球与恰有2个黑球 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
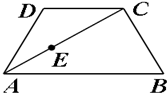 如图,等腰梯形ABCD中,$\overrightarrow{AB}=2\overrightarrow{DC}$,3$\overrightarrow{AE}=2\overrightarrow{EC}$.一双曲线经过C,D,E三点,且以A,B为焦点,则该双曲线离心率是$\sqrt{7}$.
如图,等腰梯形ABCD中,$\overrightarrow{AB}=2\overrightarrow{DC}$,3$\overrightarrow{AE}=2\overrightarrow{EC}$.一双曲线经过C,D,E三点,且以A,B为焦点,则该双曲线离心率是$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com