
【题目】如图,已知几何体的三视图(单位:cm).
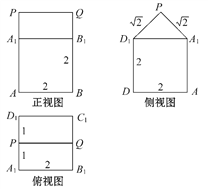
(1)画出这个几何体的直观图(不要求写画法).
(2)求这个几何体的表面积及体积.
科目:高中数学 来源: 题型:
【题目】知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在区间[t,t+2](t>0)上的最小值;
(2)对一切实数x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明对一切x∈(0,+∞),lnx> ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥☉O所在的平面,AB是☉O的直径,C是☉O上的一点,AE⊥PB于E,AF⊥PC于F,给出下列结论:①BC⊥平面PAC;②AF⊥平面PCB;③EF⊥PB;④AE⊥平面PBC.其中正确命题的个数是( )
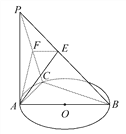
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
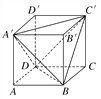
(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(x﹣1)的对称轴为x=1,f(x+1)= ![]() (f(x)≠0),且在区间(1,2)上单调递减,已知α、β是钝角三角形中两锐角,则f(sinα)和f(cosβ)的大小关系是( )
(f(x)≠0),且在区间(1,2)上单调递减,已知α、β是钝角三角形中两锐角,则f(sinα)和f(cosβ)的大小关系是( )
A.f(sinα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(sinα)=f(cosβ)
D.以上情况均有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在两块钢板上打孔,用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一端锤打出一个帽,使得与钉帽的大小相等.铆合的两块钢板,成为某种钢结构的配件,其截面图如图2.(单位:mm,加工中不计损失).
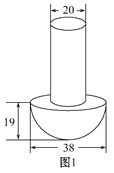
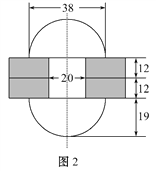
(1)若钉身高度是钉帽高度的2倍,求铆钉的表面积.
(2)若每块钢板的厚度为12mm,求钉身的长度(结果精确到1 mm).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是甲、乙两人在一次射击比赛中中靶的情况(击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中所得的环数),每人射击了6次.
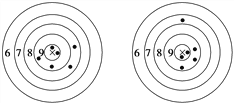
甲射击的靶 乙射击的靶
(1)请用列表法将甲、乙两人的射击成绩统计出来;
(2)请你用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() 是定义在[-l,1]上的奇函数,且f(
是定义在[-l,1]上的奇函数,且f(![]() )=
)=![]() 。
。
(1)确定函数f(x)的解析式;
(2)判断并用定义证明f(x)在(-1,1)上的单调性;
(3)若f(1-3m)+f(1+m)≥0,求实数m的所有可能的取值。
查看答案和解析>>
科目:高中数学 来源: 题型:
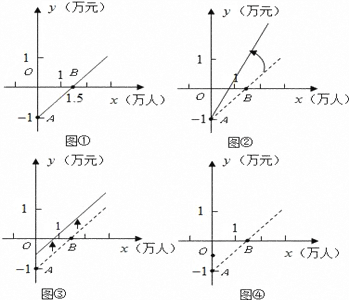
【题目】如图是某公共汽车线路收支差额(票价总收人减去运营成本)与乘客量的函数图象.目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会.乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,以此举实现扭亏.公交公司认为:运营成本难以下降,公司己尽力,提高票价才能扭亏.根据这两种意见,可以把图分别改画成图②和图③,
(1)说明图①中点![]() 和点
和点![]() 以及射线
以及射线![]() 的实际意义;
的实际意义;
(2)你认为图②和图③两个图象中,反映乘客意见的是_________,反映公交公司意见的是_________.
(3)如果公交公司采用适当提高票价又减少成本的办法实现扭亏为赢,请你在图④中画出符合这种办法的大致函数关系图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com