
【题目】在如图所示的几何体中,四边形ABCD为正方形,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() .
.
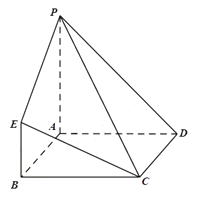
(1)求证:![]() 平面PAD;
平面PAD;
(2)在棱AB上是否存在一点F,使得平面![]() 平面PCE?如果存在,求
平面PCE?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】(1)证明见解析(2)存在,![]()
【解析】
(1)根据已知条件便可证明平面BCE∥平面PAD,从而便得到CE∥平面PAD;
(2)首先分别以AB,AD,AP三直线为x,y,z轴,建立空间直角坐标系,要使平面DEF⊥平面PCE,则有这两平面的法向量垂直,设![]() ,平面PCE的法向量为
,平面PCE的法向量为![]() ,根据
,根据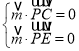 即可求出
即可求出![]() ,同样的办法表示出平面DEF的法向量
,同样的办法表示出平面DEF的法向量![]() ,根据
,根据![]() 即可求出
即可求出![]() ,从而求出
,从而求出![]() 的值.
的值.
解:(1)设PA中点为G,连结EG,DG,
因为![]() ,且
,且![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形BEGA为平行四边形,所以![]() ,且
,且![]() .
.
因为正方形ABCD,所以![]() ,
,![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形CDGE为平行四边形,所以![]() .
.
因为![]() 平面PAD,
平面PAD,![]() 平面PAD,所以
平面PAD,所以![]() 平面PAD.
平面PAD.
(2)如图,建立空间坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
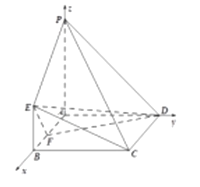
所以![]() ,
,![]() ,
,![]() .
.
设平面PCE的一个法向量为![]() ,
,
所以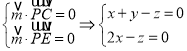
令![]() ,则,所以
,则,所以![]() .
.
假设存在点![]() 满足题意,则
满足题意,则![]() ,
,![]() .
.
设平面DEF的一个法向量为![]() ,
,
则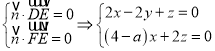 ,
,
令![]() ,则
,则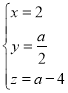 ,所以
,所以![]() .
.
因为平面![]() 平面PCE,所以
平面PCE,所以![]() ,即
,即![]() ,
,
所以![]() ,故存在点
,故存在点![]() 满足题意,且
满足题意,且![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)长轴的两顶点为A、B,左右焦点分别为F1、F2,焦距为2c且a=2c,过F1且垂直于x轴的直线被椭圆C截得的线段长为3.
(a>b>0)长轴的两顶点为A、B,左右焦点分别为F1、F2,焦距为2c且a=2c,过F1且垂直于x轴的直线被椭圆C截得的线段长为3.
(1)求椭圆C的方程;
(2)在双曲线![]() 上取点Q(异于顶点),直线OQ与椭圆C交于点P,若直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,试证明:k1+k2+k3+k4为定值;
上取点Q(异于顶点),直线OQ与椭圆C交于点P,若直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,试证明:k1+k2+k3+k4为定值;
(3)在椭圆C外的抛物线K:y2=4x上取一点E,若EF1、EF2的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司进行共享单车的投放与损耗统计,到去年![]() 年底单车的市场保有量(已投入市场且能正常使用的单车数量)为
年底单车的市场保有量(已投入市场且能正常使用的单车数量)为![]() 辆,预计今后每年新增单车1000辆,随着单车的频繁使用,估计每年将有200辆车的损耗,并且今后若干年内,年平均损耗在上一年损耗基础上增加
辆,预计今后每年新增单车1000辆,随着单车的频繁使用,估计每年将有200辆车的损耗,并且今后若干年内,年平均损耗在上一年损耗基础上增加![]() %.
%.
(1)预计![]() 年底单车的市场保有量是多少?
年底单车的市场保有量是多少?
(2)到哪一年底,市场的单车保有量达到最多?该年的单车保有量是多少辆(最后结果精确到整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率;
(2)根据统计数据估计图书分类错误的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() 、
、![]() 且
且![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.

(I)证明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com