
设A(7,1),B(1,5),P(7,14)为坐标平面上三点,0为坐标原点,点M为线段OP上的一个动点.
(I)求向量![]() 在向量
在向量![]() 方向上的投影的最小值; .
方向上的投影的最小值; .
(II)当![]() ?
?![]() 取最小值时,求点M的坐标;
取最小值时,求点M的坐标;
(III)当点M满足(2)的条件和结论时,求cos∠AMB的值.
解:(I)设M(x,y) ∵点M在线段OP上
∴o≤x≤7,且向量![]() 与
与![]() 商共线
商共线
又![]() =(x,y),
=(x,y),![]() =(7,14)
=(7,14)
∴14x一7y=0 ∴.Y=2x.∴M(x,2x)
∴![]() =(7,1)一(x,2x)=(7--x,1―2x)
=(7,1)一(x,2x)=(7--x,1―2x) ![]() = (1,5)一(7,1)=(一6,4)
= (1,5)一(7,1)=(一6,4)
∴![]() 在向量
在向量![]() 方向上的投影为:
方向上的投影为:
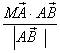 =
=![]()
∴0≤x≤7 ∴当x=7时,所求投影的最小值为![]()
(Ⅱ)由(I)知![]() =(7一x,1―2x)
=(7一x,1―2x)
又![]() =(1,5)一(x,2x)=(1―x,5―2x)
=(1,5)一(x,2x)=(1―x,5―2x)
∴![]() ?
?![]() =(7--x,1―2x)?(1一x,5―2x)
=(7--x,1―2x)?(1一x,5―2x)
=(7--x) (1一x+(1―2x)(5―2x)
=5![]() --8
--8
当x=2∈(0,7)时![]() ?
?![]() 取最小值一8,此时点M(2,4).
取最小值一8,此时点M(2,4).
(Ⅲ)由(1I)知,![]() =(5,一3),
=(5,一3),![]() =(一1,1)
=(一1,1)
Cos∠AMB= =
=![]()


科目:高中数学 来源:2011-2012学年河北省邯郸市大名三中高一(上)期中数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com