
【题目】小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为![]() ;小李后掷一枚骰子,向上的点数记为
;小李后掷一枚骰子,向上的点数记为![]() .
.
(1)求![]() 能被
能被![]() 整除的概率.
整除的概率.
(2)规定:若![]() ,则小王赢;若
,则小王赢;若![]() ,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为
(1)写出直线![]() 及曲线
及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,△
为矩形,△![]() 为等腰三角形,
为等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=![]() .
.

(1)证明:CB1⊥BA1;
(2)已知AB=2,BC=![]() ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.

(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年
的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年![]() 位居民毎人的月均用水量(单位:吨),将数据按照
位居民毎人的月均用水量(单位:吨),将数据按照![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.
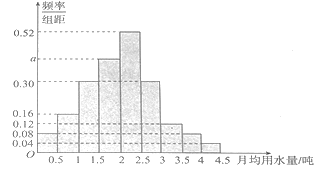
(1)求直方图中![]() 的值;
的值;
(2)若该市有![]() 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于![]() 吨的人数,并说明理由;
吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到
的值(精确到![]() ),并说明理由.
),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线上横坐标为
,抛物线上横坐标为![]() 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两条公路AP与AQ夹角A为钝角,其正弦值是![]()
![]() .甲乙两人从A点出发沿着两条公路进行搜救工作,甲沿着公路AP方向,乙沿着公路AQ方向.
.甲乙两人从A点出发沿着两条公路进行搜救工作,甲沿着公路AP方向,乙沿着公路AQ方向.

(1)当甲前进5km的时候到达P处,同时乙到达Q处,通讯测得甲乙两人相距![]()
![]() km,求乙在此时前进的距离AQ;
km,求乙在此时前进的距离AQ;
(2)甲在5公里处原地未动,乙回头往A方向行走至M点收到甲发出的信号,此时M点看P、Q两点的张角为![]() (张角为
(张角为![]() QMP)
QMP)![]() ,求甲乙两人相距的距离MP的长.
,求甲乙两人相距的距离MP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com