练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若三个点P(1，1)，A(2，－4)，B(x，－9)共线，则x＝(      )

    A.－1       B.3          C.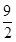            D.51

     

    【答案】

    B

    【解析】

    试题分析：三点共线问题一般可由斜率相等列出方程求参数的值，由得，∴．

    考点：三点共线问题．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出以下三个命题：
    （A）已知P（m，4）是椭圆
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）上的一点，F1、F2是左、右两个焦点，若△PF1F2的内切圆的半径为
    3
    2
    ，则此椭圆的离心率e=
    4
    5
    ；
    （B）过椭圆C：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）上的任意一动点M，引圆O：x2+y2=b2的两条切线MA、MB，切点分别为A、B，若∠BMA=
    π
    2
    ，则椭圆的离心率e的取值范围为[
    		3
    2
    ，1)    ；
    （C）已知F1（-2，0）、F2（2，0），P是直线x=-1上一动点，则以F1、F2为焦点且过点P的双曲线的离心率e的取值范围是[2，+∞）．
    其中真命题的代号是
     
    （写出所有真命题的代号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C的左、右焦点分别是F1、F2，离心率为
    		3
    2
    ，过F1且垂直于x轴的直线被椭圆C截得的线段长为1；
    （Ⅰ）求椭圆C的方程．
    （Ⅱ）若A，B，C是椭圆上的三个点，O是坐标原点，当点B是椭圆C的右顶点，且四边形OABC为菱形时，求此菱形的面积．
    （Ⅲ）设点p是椭圆C上除长轴端点外的任一点，连接PF1、PF2，设∠F1PF2的角平分线PM交椭圆C的长轴于点M（m，0），求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2015届广东汕头金山中学高二上学期期中理科数学试卷（解析版） 题型：选择题

    若三个点P(1，1)，A(2，－4)，B(x，－9)共线，则x＝(      )

    A.－1       B. 3          C. 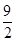            D. 51

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省高考模拟预测数学文试卷（解析版） 题型：解答题

    一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4．

    （I）从袋中随机抽取一个球，将其编号记为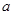，然后从袋中余下的三个球中再随机抽取一个球，将其编号记为．求关于的一元二次方程有实根的概率；

    （II）先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n．若以 作为点P的坐标，求点P落在区域内的概率．

    【解析】第一问利用古典概型概率求解所有的基本事件数共12种，然后利用方程有实根，则满足△=4a2-4b2≥0，即a2≥b2。，这样求得事件发生的基本事件数为6种，从而得到概率。第二问中，利用所有的基本事件数为16种。即基本事件（m，n）有：（1，1）  （1,2）   （1,3）  （1,4）   （2,1）  （2，2）  （2,3）   （2,4）   （3,1）   （3,2）  （3，3）    （3,4）   （4,1）   （4,2）   （4,3）  （4，4）共16种。在求解满足的基本事件数为（1，1） （2,1）  （2，2） （3,1） 共4种，结合古典概型求解得到概率。

    （1）基本事件（a，b）有：（1,2）   （1,3）  （1,4）   （2,1）   （2,3）   （2,4）   （3,1）   （3,2）  （3,4）   （4,1）   （4,2）   （4,3）共12种。

    ∵有实根， ∴△=4a2-4b2≥0，即a2≥b2。

    记“有实根”为事件A，则A包含的事件有：（2,1）   （3,1）   （3,2）  （4,1）   （4,2）   （4,3） 共6种。

    ∴PA.= 。   …………………6分

    （2）基本事件（m，n）有：（1，1）  （1,2）   （1,3）  （1,4）   （2,1）  （2，2）  （2,3）   （2,4）   （3,1）   （3,2）  （3，3）    （3,4）   （4,1）   （4,2）   （4,3）  （4，4）共16种。

    记“点P落在区域内”为事件B，则B包含的事件有：

    （1，1） （2,1）  （2，2） （3,1） 共4种。∴PB.=

     

    查看答案和解析>>

    同步练习册答案