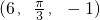练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设M（x，y，z）为空间直角坐标系内一点，点M在xOy平面上的射影P的极坐标为（ρ，θ）（极坐标系以O为极点，以x轴为极轴），则我们称三元数组（ρ，θ，z）为点M的柱面坐标．已知M点的柱面坐标为数学公式，则直线OM与xOz平面所成的角为________．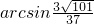


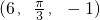    分析：根据题意：“M点的柱面坐标为，”作出立体图形，如图所示．利用长方体模型进行计算即可．在长方体OM中，∠PON=，ON=6，MN=1，直线OM与xOz平面所成的角为∠MOQ，利用长方体的性质得到对角线的长，再在直角三角形MOQ中，求出sin∠MOQ，从而得出则直线OM与xOz平面所成的角的大小．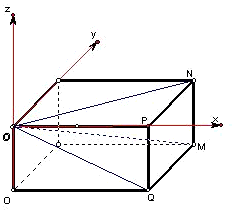
    解答：解：根据题意作出立体图形，如图所示．
    在长方体OM中，∠PON=，ON=6，MN=1，直线OM与xOz平面所成的角为∠MOQ，
    在直角三角形OPN中，OP=ONcos=3，PN=ONsin=3，
    ∴OM===，
    在直角三角形MOQ中，sin∠MOQ===．
    ∴则直线OM与xOz平面所成的角∠MOQ为．
    故答案为：．
    点评：本题考查直线与平面所成的角和线面角，本题解题的关键是构造长方体，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

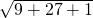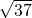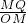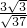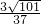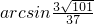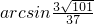    科目：高中数学 来源： 题型：

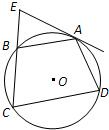    精英家教网附加题：
    A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
    求证：AB2=BE•CD．
    B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足
    an+4
    bn+4
    =M
    an
    bn
    ，试求二阶矩阵M．
    C．已知椭圆C的极坐标方程为ρ2=
    12
    3cos2θ+4sin2θ
    ，点F1，F2为其左、右焦点，直线l的参数方程为
    x=2+
    		2
    2
    t
    y=
    		2
    2
    t
    （t为参数，t∈R）．求点F1，F2到直线l的距离之和．
    D．已知x，y，z均为正数．求证：
    x
    yz
    +
    y
    zx
    +
    z
    xy
    ≥
    1
    x
    +
    1
    y
    +
    1
    z
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•闸北区二模）设M（x，y，z）为空间直角坐标系内一点，点M在xOy平面上的射影P的极坐标为（ρ，θ）（极坐标系以O为极点，以x轴为极轴），则我们称三元数组（ρ，θ，z）为点M的柱面坐标．已知M点的柱面坐标为(6，
    π
    3
    ，-1)    ，则直线OM与xOz平面所成的角为
    arcsin
    3
    		101
    37
    arcsin
    3
    		101
    37
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010年江苏省泰州高级中学高考数学模拟试卷（解析版） 题型：解答题

    附加题：
    A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
    求证：AB2=BE•CD．
    B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足=M，试求二阶矩阵M．
    C．已知椭圆C的极坐标方程为，点F1，F2为其左、右焦点，直线l的参数方程为（t为参数，t∈R）．求点F1，F2到直线l的距离之和．
    D．已知x，y，z均为正数．求证：．

    查看答案和解析>>

    科目：高中数学 来源：2013年上海市闸北区高考数学二模试卷（理科）（解析版） 题型：填空题

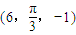    设M（x，y，z）为空间直角坐标系内一点，点M在xOy平面上的射影P的极坐标为（ρ，θ）（极坐标系以O为极点，以x轴为极轴），则我们称三元数组（ρ，θ，z）为点M的柱面坐标．已知M点的柱面坐标为，则直线OM与xOz平面所成的角为    ．

    查看答案和解析>>

    同步练习册答案