
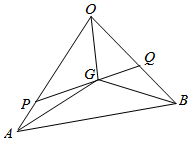
 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.分析 (1)延长OG交AB于D,即有D为AB的中点,应用重心的性质和中点向量表示,可得$\overrightarrow{OG}$;
(2)由已知条件求得$\overrightarrow{a}$、$\overrightarrow{b}$,结合(1)的结论,应用三点共线的向量表示,其系数和为1,即可得到所求定值.
解答 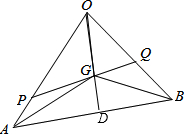 解:(1)点G是△OAB的重心,
解:(1)点G是△OAB的重心,
延长OG交AB于D,即有D为AB的中点,
可得$\overrightarrow{OG}$=$\frac{2}{3}$$\overrightarrow{OD}$=$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\frac{1}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$);
(2)$\frac{1}{m}$+$\frac{1}{n}$为定值3.
理由:由$\overrightarrow{OP}$=m$\overrightarrow{a}$,$\overrightarrow{OQ}$=n$\overrightarrow{b}$,
可得$\overrightarrow{a}$=$\frac{1}{m}$$\overrightarrow{OP}$,$\overrightarrow{b}$=$\frac{1}{n}$$\overrightarrow{OQ}$,
即有$\overrightarrow{OG}$=$\frac{1}{3m}$$\overrightarrow{OP}$+$\frac{1}{3n}$$\overrightarrow{OQ}$,
由三点P,G,Q共线,可得$\frac{1}{3m}$+$\frac{1}{3n}$=1,
即为$\frac{1}{m}$+$\frac{1}{n}$=3.
则$\frac{1}{m}$+$\frac{1}{n}$为定值3.
点评 本题考查平面向量和应用,主要是向量共线定理和三点共线的向量表示,考查运算能力,属于中档题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
 某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=b<c | B. | b=c<a | C. | a=c<b | D. | a=b=c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )
如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | 7 | C. | -12 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 中位数 | B. | 众数 | C. | 方差 | D. | 频率分布 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥β,则α⊥β | B. | 若α⊥γ,β⊥γ,则α∥β | C. | 若m∥α,m∥β,则α∥β | D. | 若m⊥α,n∥α,则m⊥n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com