
【题目】已知向量![]() ,设
,设![]() .
.
(1)求函数![]() 的解析式及单调递增区间;
的解析式及单调递增区间;
(2)在![]() 中,
中,![]() 分别为内角
分别为内角![]() 的对边,且
的对边,且![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)[-![]() ]
]![]() ;(2)面积为
;(2)面积为 ![]() .
.
【解析】分析:(I)根据向量数量积的坐标公式得出f(x),利用二倍角公式,两角和的正弦函数公式化简,根据正弦函数的单调性得出f(x)的单调区间;
(II)根据f(A)=1和A的范围解出A,利用余弦定理得出bc,代入面积公式S=![]() bcsinA即可.
bcsinA即可.
详解:(I)f(x)=![]() sinxcosx+cos2x=
sinxcosx+cos2x=![]() sin2x+
sin2x+![]() cos2x+
cos2x+![]() =
=![]() .
.
![]() ,
,![]() .得[-
.得[-![]() ]
]![]() .
.
所以函数的单调递增区间为[-![]() ]
]![]() .
.
(II)∵f(A)=sin(2A+![]() )+
)+![]() =1,∴sin(2A+
=1,∴sin(2A+![]() )=
)=![]() .
.
∵0<A<π,∴![]() <2A+
<2A+![]() <
<![]() ,∴2A+
,∴2A+![]() =
=![]() ,即A=
,即A=![]() .
.
由余弦定理得:a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA,∴1=4﹣3bc,∴bc=1.
∴![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,且f(x)=x有唯一解,
,且f(x)=x有唯一解,![]() ,xn+1=f(xn)(n∈N*).
,xn+1=f(xn)(n∈N*).
(1)求实数a的值;
(2)求数列{xn}的通项公式;
(3)若![]() ,数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为
,数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为![]() 的等比数列,记cn=anbn,求数列{cn}的前n项和Sn.
的等比数列,记cn=anbn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xln(1+x)﹣a(x+1),其中a为实常数.
(1)当x∈[1,+∞)时,f′(x)>0恒成立,求a的取值范围;
(2)求函数 ![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,已知
中,已知![]() ,
,![]() (n∈N*)
(n∈N*)
(1)求数列![]() 的通项公式
的通项公式
(2)若![]() (λ为非零常数),问是否存在整数λ使得对任意n∈N*都有
(λ为非零常数),问是否存在整数λ使得对任意n∈N*都有![]() ?若存在,求出λ的值;若不存在,请说明理由.
?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)
分)
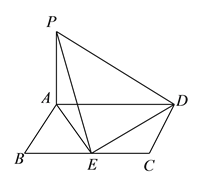
如图,平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 中点,连结
中点,连结![]() 、
、![]() .
.
(Ⅰ)若![]() ,
, ![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,试探究在直线
,试探究在直线![]() 上有几个点
上有几个点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,直线
,直线![]() 与
与![]() 的图象的相邻两个交点的横坐标分别是
的图象的相邻两个交点的横坐标分别是![]() 和
和![]() ,现有如下命题:
,现有如下命题:
①该函数在![]() 上的值域是
上的值域是![]() ;
;
②在![]() 上,当且仅当
上,当且仅当![]() 时函数取最大值;
时函数取最大值;
③该函数的最小正周期可以是![]() ;
;
④![]() 的图象可能过原点.
的图象可能过原点.
其中的真命题有__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于155 ![]() 到195
到195![]() 之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,并按此分组绘制如图所示的频率分布直方图,其中第六组
,并按此分组绘制如图所示的频率分布直方图,其中第六组![]() 和第七组
和第七组![]() 还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
(1)补全频率分布直方图;
(2)根据频率分布直方图估计这50位男生身高的中位数;
(3)用分层抽样的方法在身高为![]() 内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在
内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在![]() 内的概率.
内的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com