
°ĺŐ‚ńŅ°Ņ–¬“©‘ŕĹÝ»ŽŃŔī≤ Ķ—ť÷ģ«į£¨–Ť“™Ō»Õ®Ļż∂ĮőÔĹÝ––”––ß–‘ļÕį≤»ę–‘Ķń Ķ—ť£ģŌ÷∂‘ń≥÷÷–¬“©ĹÝ––5000īő∂ĮőÔ Ķ—ť£¨“Ľīő Ķ—ť∑Ĺįł»ÁŌ¬£ļ—°»°3÷Ľį◊ ů∂‘“©–ßĹÝ––ľž—ť£¨ĶĪ3÷Ľį◊ ů÷–”–2÷ĽĽÚ2÷Ľ“‘…Ō Ļ”√°į–ßĻŻ√ųŌ‘°Ī£¨ľī»∑∂®°į Ķ—ť≥…Ļ¶°Ī£Ľ»Ű”–«“÷Ľ”–1÷Ľ°į–ßĻŻ√ųŌ‘°Ī£¨‘Ú‘Ŕ»°2÷Ľį◊ ůĹÝ––∂Ģīőľž—ť£¨ĶĪ2÷Ľį◊ ůĺý Ļ”√°į–ßĻŻ√ųŌ‘°Ī£¨ľī»∑∂®°į Ķ—ť≥…Ļ¶°Ī£¨∆š”ŗ«ťŅŲ‘Ú»∑∂®°į Ķ—ť ßį‹°Ī£ģ…Ť∂‘√Ņ÷Ľį◊ ůĶń Ķ—ťŌŗĽ•∂ņŃĘ£¨«“ Ļ”√°į–ßĻŻ√ųŌ‘°ĪĶńłŇ¬ ĺýő™![]() £ģ
£ģ
£®ĘŮ£©»Ű![]() £¨…Ťł√–¬“©‘ŕ“Ľīő Ķ—ť∑Ĺįł÷–°į Ķ—ť≥…Ļ¶°ĪĶńłŇ¬ ő™
£¨…Ťł√–¬“©‘ŕ“Ľīő Ķ—ť∑Ĺįł÷–°į Ķ—ť≥…Ļ¶°ĪĶńłŇ¬ ő™![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®ĘÚ£©»Ű∂ĮőÔ Ķ—ť‘§ň„ĺ≠∑—700ÕÚ‘™£¨∂‘√Ņ÷Ľį◊ ůĹÝ–– Ķ—ť–Ť“™300‘™£¨∆šňŻ∑—”√◊‹ľ∆ő™100ÕÚ‘™£¨ő ł√∂ĮőÔ Ķ—ť◊‹∑—”√ «∑ŮĽŠ≥¨≥Ų‘§ň„£¨≤ĘňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®ĘŮ£©![]() £Ľ£®ĘÚ£©ł√Ĺ◊∂őĺ≠∑— Ļ”√≤ĽĽŠ≥¨≥Ų‘§ň„£¨ņŪ”…ľŻĹ‚őŲ.
£Ľ£®ĘÚ£©ł√Ĺ◊∂őĺ≠∑— Ļ”√≤ĽĽŠ≥¨≥Ų‘§ň„£¨ņŪ”…ľŻĹ‚őŲ.
°ĺĹ‚őŲ°Ņ
£®ĘŮ£©łý囼•≥‚ ¬ľĢĶńłŇ¬ £¨«ů“Ľīőľž—ť≥…Ļ¶ļÕĺ≠ĻżŃĹīőľž—ť≤Ň≥…Ļ¶ĶńłŇ¬ ÷ģļÕľīŅ…«ůĹ‚£Ľ£®ĘÚ£©…Ť“Ľīő Ķ—ť∑Ĺįł–Ť“™”√ĶĹĶńĺ≠∑—ő™![]() ‘™£¨”…Ő‚“‚Ņ…÷™
‘™£¨”…Ő‚“‚Ņ…÷™![]() ĶńŅ…ń‹÷Ķő™900£¨1500£¨«ůňśĽķĪšŃŅĶń∆ŕÕŻ£¨ņŻ”√Ķľ ż«ů≥Ų∆ŕÕŻĶń◊Óīů÷Ķ£¨ľīŅ…«ů◊‹∑—”√Ķń◊Óīů÷Ķ£¨Ķ√≥ŲĹŠ¬Ř.
ĶńŅ…ń‹÷Ķő™900£¨1500£¨«ůňśĽķĪšŃŅĶń∆ŕÕŻ£¨ņŻ”√Ķľ ż«ů≥Ų∆ŕÕŻĶń◊Óīů÷Ķ£¨ľīŅ…«ů◊‹∑—”√Ķń◊Óīů÷Ķ£¨Ķ√≥ŲĹŠ¬Ř.
£®ĘŮ£©ĶĪ![]() Ī£¨“Ľīőľž—ťĺÕ»°Ķ√°į Ķ—ť≥…Ļ¶°ĪĶńłŇ¬ ő™
Ī£¨“Ľīőľž—ťĺÕ»°Ķ√°į Ķ—ť≥…Ļ¶°ĪĶńłŇ¬ ő™![]() £Ľ
£Ľ
ĺ≠ĻżŃĹīőľž—ť≤Ň»°Ķ√°į Ķ—ť≥…Ļ¶°ĪĶńłŇ¬ ő™![]() £Ľ
£Ľ
‘ŕ“Ľīő Ķ—ť∑Ĺįł÷–°į Ķ—ť≥…Ļ¶°ĪĶńłŇ¬ ő™![]() £ģ
£ģ
£®ĘÚ£©…Ť“Ľīő Ķ—ť∑Ĺįł–Ť“™”√ĶĹĶńĺ≠∑—ő™![]() ‘™£¨‘Ú
‘™£¨‘Ú![]() ĶńŅ…ń‹÷Ķő™900£¨1500£ģ
ĶńŅ…ń‹÷Ķő™900£¨1500£ģ
![]() £Ľ
£Ľ![]() £ģ
£ģ
ňý“‘![]() £¨
£¨
…Ť![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨
ĶĪ![]() Ī£¨
Ī£¨![]() £¨ňý“‘
£¨ňý“‘![]() ‘ŕ
‘ŕ![]() …ŌĶ•‘Ų£Ľ
…ŌĶ•‘Ų£Ľ
ĶĪ![]() Ī£¨
Ī£¨![]() £¨ňý“‘
£¨ňý“‘![]() ‘ŕ
‘ŕ![]() …ŌĶ•ľű£ģ
…ŌĶ•ľű£ģ
ňý“‘![]() Ķń◊Óīů÷Ķő™
Ķń◊Óīů÷Ķő™![]() £¨
£¨
“Úīň Ķ ©“Ľīőīň∑Ĺįł◊ÓłŖ∑—”√ő™![]() ‘™
‘™
ňý“‘∂ĮőÔ Ķ—ťĹ◊∂őĻņľ∆◊ÓłŖ ‘—ť∑—”√ő™![]() ÕÚ‘™£¨
ÕÚ‘™£¨
“Úő™![]() £¨
£¨
ňý“‘ł√Ĺ◊∂őĺ≠∑— Ļ”√≤ĽĽŠ≥¨≥Ų‘§ň„£ģ


 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨Ň◊őÔŌŖ
÷–£¨Ň◊őÔŌŖ![]() ĶńĹĻĶ„ő™
ĶńĹĻĶ„ő™![]() £¨
£¨![]() (∆š÷–
(∆š÷–![]() ) «
) «![]() …ŌĶń“ĽĶ„£¨«“
…ŌĶń“ĽĶ„£¨«“![]() .
.
(1)«ůŇ◊őÔŌŖ![]() Ķń∑Ĺ≥Ő£Ľ
Ķń∑Ĺ≥Ő£Ľ
(2)“—÷™![]() ő™Ň◊őÔŌŖ
ő™Ň◊őÔŌŖ![]() …Ō≥ż∂•Ķ„
…Ō≥ż∂•Ķ„![]() ÷ģÕ‚Ķń»ő“‚“ĽĶ„£¨‘ŕĶ„
÷ģÕ‚Ķń»ő“‚“ĽĶ„£¨‘ŕĶ„![]() ī¶Ķń«–ŌŖ”Ž
ī¶Ķń«–ŌŖ”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() £¨Ļż
£¨Ļż![]() Ķ„Ķń÷ĪŌŖ
Ķ„Ķń÷ĪŌŖ![]() ĹĽŇ◊őÔŌŖ”ŕ
ĹĽŇ◊őÔŌŖ”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨…Ť
ŃĹĶ„£¨…Ť![]() £¨
£¨![]() £¨
£¨![]() Ķń–Ī¬ ∑÷Īūő™
Ķń–Ī¬ ∑÷Īūő™![]() £¨
£¨![]() £¨
£¨![]() £¨«ů÷§£ļ
£¨«ů÷§£ļ![]() £¨
£¨![]() £¨
£¨![]() ≥…Ķ»Ī» żŃ–.
≥…Ķ»Ī» żŃ–.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ2019ńÍ12‘¬1»’∆ū÷£÷› – ©––°∂÷£÷› –≥« –…ķĽÓņ¨ĽÝ∑÷ņŗĻ‹ņŪįž∑®°∑£¨÷£÷›Ĺę’ż ĹĹÝ»Ž≥« –…ķĽÓņ¨ĽÝ∑÷ņŗ Īīķ£ģő™Ńň‘Ų«Ņ…Á«Ýĺ”√Ů∂‘ņ¨ĽÝ∑÷ņŗ÷™ ∂ĶńŃňĹ‚£¨Ľżľę≤ő”ŽĶĹņ¨ĽÝ∑÷ņŗĶń––∂Į÷–£¨ń≥…Á«Ý≤…”√ŌŖŌ¬ļÕŌŖ…ŌŌŗĹŠļŌĶń∑Ĺ ĹŅ™’ĻŃň“Ľīő200√ŻŌĹ«Ý≥…‘Ī≤őľ”Ķń°įņ¨ĽÝ∑÷ņŗ”–Ļō÷™ ∂°Ī◊®Ő‚Ňŗ—Ķ£ģő™ŃňŃňĹ‚≤ő—Ķ≥…‘Ī∂‘”ŕŌŖ…ŌŇŗ—Ķ°ĘŌŖŌ¬Ňŗ—ĶĶń¬ķ“‚≥Ő∂»£¨…Á«Ýĺ”őĮĽŠňśĽķ—°»°Ńň40√ŻŌĹ«Ý≥…‘Ī£¨ĹęňŻ√«∑÷≥…ŃĹ◊ť£¨√Ņ◊ť20»ň£¨∑÷Īū∂‘ŌŖ…Ō°ĘŌŖŌ¬ŃĹ÷÷Ňŗ—ĶĹÝ––¬ķ“‚∂»≤‚∆ņ£¨łýĺ›ŌĹ«Ý≥…‘ĪĶń∆ņ∑÷£®¬ķ∑÷100∑÷£©Ľś÷∆Ńň»ÁÕľňý ĺĶńĺ•“∂Õľ£ģ
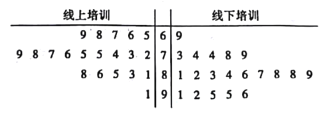
£®1£©łýĺ›ĺ•“∂ÕľŇ–∂ŌŌĹ«Ý≥…‘Ī∂‘”ŕŌŖ…Ō°ĘŌŖŌ¬ńń÷÷Ňŗ—ĶĶń¬ķ“‚∂»łŁłŖ£¨≤ĘňĶ√ųņŪ”…£ģ
£®2£©«ů’‚40√ŻŌĹ«Ý≥…‘Ī¬ķ“‚∂»∆ņ∑÷Ķń÷–őĽ ż![]() £¨≤ĘĹę∆ņ∑÷≤Ľ≥¨Ļż
£¨≤ĘĹę∆ņ∑÷≤Ľ≥¨Ļż![]() °Ę≥¨Ļż
°Ę≥¨Ļż![]() ∑÷Īū ”ő™°įĽýĪĺ¬ķ“‚°Ī°į∑«≥£¬ķ“‚°ĪŃĹłŲĶ»ľ∂£ģ
∑÷Īū ”ő™°įĽýĪĺ¬ķ“‚°Ī°į∑«≥£¬ķ“‚°ĪŃĹłŲĶ»ľ∂£ģ
£®Ę°£©ņŻ”√—ýĪĺĻņľ∆◊‹ŐŚĶńňľŌŽ£¨Ļņň„ĪĺīőŇŗ—ĶĻ≤”–∂ŗ…ŔŌĹ«Ý≥…‘Ī∂‘ŌŖ…ŌŇŗ—Ķ∑«≥£¬ķ“‚£Ľ
£®ĘĘ£©łýĺ›ĺ•“∂ÕľŐÓ–īŌ¬√śĶńŃ–Ń™ĪŪ£ģ
ĽýĪĺ¬ķ“‚ | ∑«≥£¬ķ“‚ | ◊‹ľ∆ | |
ŌŖ…ŌŇŗ—Ķ | |||
ŌŖŌ¬Ňŗ—Ķ | |||
◊‹ľ∆ |
≤Ęłýĺ›Ń–Ń™ĪŪŇ–∂Ōń‹∑Ů”–99£ģ5%Ķńį—ő’»Ōő™ŌĹ«Ý≥…‘Ī∂‘ŃĹ÷÷Ňŗ—Ķ∑Ĺ ĹĶń¬ķ“‚∂»”–≤Ó“ž£Ņ
łĹ£ļ
| 0£ģ010 | 0£ģ005 | 0£ģ001 |
| 6£ģ635 | 7 | 10£ģ828 |
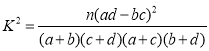 £¨∆š÷–
£¨∆š÷–![]() £ģ
£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤![]() ĶńņŽ–ń¬
ĶńņŽ–ń¬ ![]() £¨«“ĺ≠ĻżĶ„
£¨«“ĺ≠ĻżĶ„![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() ő™Õ÷‘≤ĶńňńłŲ∂•Ķ„£®»ÁÕľ£©£¨÷ĪŌŖ
ő™Õ÷‘≤ĶńňńłŲ∂•Ķ„£®»ÁÕľ£©£¨÷ĪŌŖ![]() Ļż”“∂•Ķ„
Ļż”“∂•Ķ„![]() «“īĻ÷Ī”ŕ
«“īĻ÷Ī”ŕ![]() ÷Š£ģ
÷Š£ģ
£®1£©«ůł√Õ÷‘≤ĶńĪÍ◊ľ∑Ĺ≥Ő£Ľ
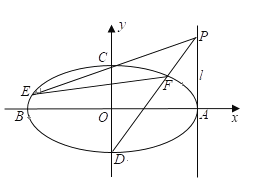
£®2£©![]() ő™
ő™![]() …Ō“ĽĶ„£®
…Ō“ĽĶ„£®![]() ÷Š…Ō∑Ĺ£©£¨÷ĪŌŖ
÷Š…Ō∑Ĺ£©£¨÷ĪŌŖ![]() £¨
£¨![]() ∑÷ĪūĹĽÕ÷‘≤”ŕ
∑÷ĪūĹĽÕ÷‘≤”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨»Ű
ŃĹĶ„£¨»Ű![]() £¨«ůĶ„
£¨«ůĶ„![]() Ķń◊ÝĪÍ£ģ
Ķń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥“Ý––Õ∆Ōķľ◊°Ę““ŃĹ÷÷ņŪ≤∆≤ķ∆∑£®√Ņ÷÷≤ķ∆∑ŌřĻļ30ÕÚ£©.√Ņ“ĽľĢ≤ķ∆∑łýĺ›∂©Ķ•Ĺū∂Ó≤ĽÕ¨Ľģ∑÷ő™£ļ∂©Ķ•Ĺū∂Ó≤ĽĶÕ”ŕ20ÕÚő™īů∂Ó∂©Ķ•£¨ĶÕ”ŕ20ÕÚő™∆’Õ®∂©Ķ•.“Ýľŗ≤Ņ√ŇňśĽķĶų»°Ļļ¬Ú’‚ŃĹ÷÷≤ķ∆∑ĶńŅÕĽßłų100Ľß£¨∂‘ňŻ√«Ķń∂©Ķ•ĹÝ––∑÷őŲ£¨Ķ√ĶĹ»ÁÕľňý ĺĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£ļ
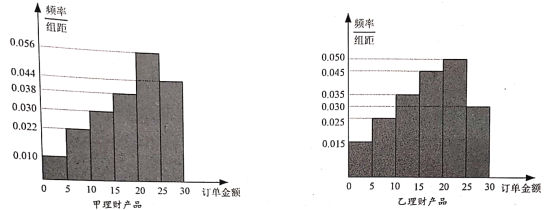
Ĺęīň—ýĪĺĶń∆Ķ¬ Ļņľ∆ ”ő™◊‹ŐŚĶńłŇ¬ .Ļļ¬Ú“ĽľĢľ◊≤ķ∆∑£¨»Ű «īů∂Ó∂©Ķ•Ņ…”ĮņŻ2ÕÚ‘™£¨»Ű «∆’Õ®∂©Ķ•‘ÚŅųňū1ÕÚ‘™£¨Ļļ¬Ú“ĽľĢ““≤ķ∆∑£¨»Ű «īů∂Ó∂©Ķ•Ņ…”ĮņŻ1.5ÕÚ‘™£¨»Ű «∆’Õ®∂©Ķ•‘ÚŅųňū0.5ÕÚ‘™.
£®1£©ľ«Xő™Ļļ¬Ú1ľĢľ◊≤ķ∆∑ļÕ1ľĢ““≤ķ∆∑ňýĶ√Ķń◊‹ņŻ»ů£¨«ůňśĽķĪšŃŅXĶń ż—ß∆ŕÕŻ£Ľ
£®2£©ľŔ…ŤĻļ¬Ú4ľĢľ◊≤ķ∆∑ļÕ4ľĢ““≤ķ∆∑ňýĽŮĶ√ĶńņŻ»ůŌŗĶ».
£®i£©’‚4ľĢľ◊≤ķ∆∑ļÕ4ľĢ““≤ķ∆∑÷–łų”–īů∂Ó∂©Ķ•∂ŗ…ŔľĢ?
£®ĘĘ£©’‚4ľĢľ◊≤ķ∆∑ļÕ4ľĢ““≤ķ∆∑÷–īů∂Ó∂©Ķ•ĶńłŇ¬ ńńłŲīů?
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ°ųABC÷–£¨ńŕĹ«A£¨B£¨Cňý∂‘ĶńĪŖ∑÷Īūő™a£¨b£¨c£¨cosB£Ĺ![]() £ģ
£ģ
£®ĘŮ£©»Űc£Ĺ2a£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®ĘÚ£©»ŰC£≠B£Ĺ![]() £¨«ůsinAĶń÷Ķ£ģ
£¨«ůsinAĶń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() .
.
£®1£©Ő÷¬Ř![]() ĶńĶ•Ķų–‘£Ľ
ĶńĶ•Ķų–‘£Ľ
£®2£©Ő÷¬Ř![]() ‘ŕ
‘ŕ![]() …ŌĶńŃ„Ķ„łŲ ż.
…ŌĶńŃ„Ķ„łŲ ż.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ»ŮĹ«°ųABC÷–£¨a£Ĺ2![]() £¨_______£¨«ů°ųABCĶń÷‹≥§lĶń∑∂őߣģ
£¨_______£¨«ů°ųABCĶń÷‹≥§lĶń∑∂őߣģ
‘ŕĘŔ![]() (©Ācos
(©Ācos![]() £¨sin
£¨sin![]() )£¨
)£¨![]() (cos
(cos![]() £¨sin
£¨sin![]() )£¨«“
)£¨«“![]()
![]() £¨ĘŕcosA(2b©Āc)£ĹacosC£¨ĘŘf(x)£Ĺcosxcos(x
£¨ĘŕcosA(2b©Āc)£ĹacosC£¨ĘŘf(x)£Ĺcosxcos(x![]() )
)![]() £¨f(A)
£¨f(A)![]()
◊Ę£ļ’‚»żłŲŐűľĢ÷–»ő—°“ĽłŲ£¨≤Ļ≥š‘ŕ…Ō√śő Ő‚÷–≤Ę∂‘∆šĹÝ––«ůĹ‚£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() .
.
£®1£©»Ű![]() £¨«ůļĮ ż
£¨«ůļĮ ż![]() ‘ŕ
‘ŕ![]() ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
£®2£©Ő÷¬Ř![]() ľę÷ĶĶ„ĶńłŲ ż£Ľ
ľę÷ĶĶ„ĶńłŲ ż£Ľ
£®3£©»Ű![]() «
«![]() Ķń“ĽłŲľę–°÷ĶĶ„£¨«“
Ķń“ĽłŲľę–°÷ĶĶ„£¨«“![]() £¨÷§√ų£ļ
£¨÷§√ų£ļ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com