
【题目】已知椭圆C关于x轴、y轴都对称,并且经过两点![]() ,
,
(1)求椭圆C的离心率和焦点坐标;
(2)D是椭圆C上到点A最远的点,椭圆C在点B处的切线l与y轴交于点E,求△BDE外接圆的圆心坐标.
【答案】(1)离心率![]() ,焦点坐标为
,焦点坐标为![]() ;(2)
;(2)![]()
【解析】
(1)根据已知设所求椭圆方程为![]() ,点
,点![]() 坐标代入椭圆方程,求解得到椭圆的标准方程,即可求出离心率和焦点坐标;
坐标代入椭圆方程,求解得到椭圆的标准方程,即可求出离心率和焦点坐标;
(2)设![]() ,利用点
,利用点![]() 在椭圆上,将
在椭圆上,将![]() 表示为关于
表示为关于![]() 的二次函数,求出
的二次函数,求出![]() 最大时
最大时![]() 点坐标;显然椭圆C在点B处的切线l的斜率存在,设出其方程,与椭圆方程联立,利用
点坐标;显然椭圆C在点B处的切线l的斜率存在,设出其方程,与椭圆方程联立,利用![]() ,求出切线
,求出切线![]() 的斜率,进而求出点
的斜率,进而求出点![]() 坐标,利用待定系数法求出△BDE外接圆的一般式方程,即可得出结论.
坐标,利用待定系数法求出△BDE外接圆的一般式方程,即可得出结论.
(1)已知椭圆C关于![]() 轴、
轴、![]() 轴都对称,
轴都对称,
设其方程为![]()
由![]() 在椭圆上,得
在椭圆上,得![]() ,
,
联立解得![]() ,
,![]() ,得椭圆C的方程是
,得椭圆C的方程是![]() .
.
用![]() 依次表示椭圆的长半轴、短半轴、半焦距,
依次表示椭圆的长半轴、短半轴、半焦距,
则![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
所以,椭圆C的离心率![]() ,焦点坐标为
,焦点坐标为![]()
(2)设![]() ,则
,则![]() ,即
,即![]() ,
,
![]()
![]()
![]() .
.
函数![]() 在区间
在区间![]() 上递减,
上递减,
则![]() 取最大时,
取最大时,![]() ,此时
,此时![]() ,
,
所以,椭圆C上到点![]() 最远的点是
最远的点是![]() ;
;
设椭圆C在点![]() 处的切线
处的切线![]() 的方程为
的方程为![]() ,
,
即![]() ,与
,与![]() 联立消去
联立消去![]() 后整理得
后整理得![]() ,
,
判别式![]() ,
,
由相切条件得![]() ,
,![]() ,
,
所以椭圆C在点![]() 处的切线
处的切线![]() 的方程是
的方程是![]() ,
,
令![]() 得
得![]() ,得切线
,得切线![]() 与
与![]() 轴的交点坐标
轴的交点坐标![]() .
.
设![]() 外接圆的方程为
外接圆的方程为![]() ,
,
由三点![]()
![]() 都在圆上,
都在圆上,
得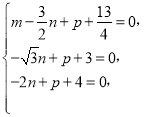 解得
解得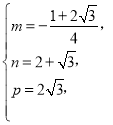
![]() ,
,![]() ,
,
所以![]() 外接圆的圆心坐标是
外接圆的圆心坐标是![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
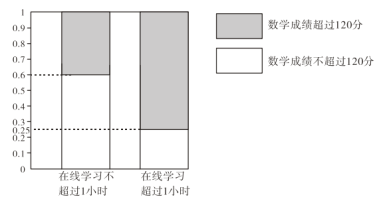
(Ⅰ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
(Ⅱ)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
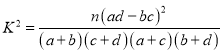
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人们通常以分贝(符号是![]() )为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为
)为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为![]() 的声音对应的等级为
的声音对应的等级为![]() ,则有
,则有![]() ,则
,则![]() 的声音与
的声音与![]() 的声音强度之比为( )
的声音强度之比为( )
A.10B.100C.1000D.10000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对
,对![]() ∈[0, π],都有
∈[0, π],都有![]() ,满足f(x2)=0的实数x有且只有3个,给出下述四个结论:①满足题目条件的实数x0有且只有1个;②满足题目条件的实数x1有且只有1个;③f(x)在
,满足f(x2)=0的实数x有且只有3个,给出下述四个结论:①满足题目条件的实数x0有且只有1个;②满足题目条件的实数x1有且只有1个;③f(x)在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() ;其中所有正确结论的编号是( )
;其中所有正确结论的编号是( )
A.①③B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (其中
(其中![]() ,m,n为常数)
,m,n为常数)
(1)当![]() 时,对
时,对![]() 有
有![]() 恒成立,求实数n的取值范围;
恒成立,求实数n的取值范围;
(2)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() 的零点为
的零点为![]() ,求所有满足
,求所有满足![]() 的整数k的和.
的整数k的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了科学防疫知识竞赛.经过选拔,甲、乙、丙三位选手进入了最后角逐.他们还将进行四场知识竞赛.规定:每场知识竞赛前三名的得分依次为a,b,c(![]() ,且a,b,
,且a,b,![]() );选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
);选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解该校学生“停课不停学”的网络学习效率,随机抽查了高一年级100位学生的某次数学成绩,得到如图所示的频率分布直方图:
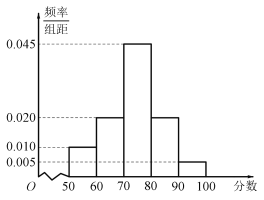
(1)估计这100位学生的数学成绩的平均值![]() .(同一组中的数据用该组区间的中点值代表);
.(同一组中的数据用该组区间的中点值代表);
(2)根据整个年级的数学成绩,可以认为学生的数学成绩![]() 近似地服从正态分布
近似地服从正态分布![]() 经计算,(1)问中样本标准差
经计算,(1)问中样本标准差![]() 的近似值为10.用样本平均数
的近似值为10.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
参考数据:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]()
(3)该年级1班的数学老师为了能每天督促学生的网络学习,提高学生每天的作业质量及学习数学的积极性,特意在微信上设计了一个每日作业小程序,每当学生提交的作业获得优秀时,就有机会参与一次小程序中“玩游戏,得奖励积分”的活动,开学后可根据获得积分的多少领取老师相应的小奖品.小程序页面上有一列方格,共15格,刚开始有只小兔子在第1格,每点一下游戏的开始按钮,小兔子就沿着方格跳一下,每次跳1格或跳2格,概率均为![]() ,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第
,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求
是等比数列,并求![]() 的值.(获胜的概率)
的值.(获胜的概率)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com