
 .
.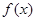 的单调性;
的单调性;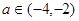 及
及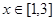 时,恒有
时,恒有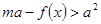 成立,求实数
成立,求实数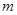 的取值范围.
的取值范围. 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:填空题
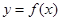 满足:
满足: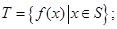 (ii)对任意
(ii)对任意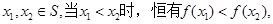
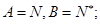
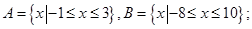
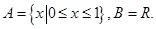
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
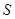 的最大允许值是多少?
的最大允许值是多少?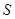 达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
达到最大而实际投入又不超过预算,正面铁栅应设计为多长?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
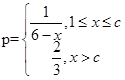 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
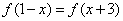 ,且
,且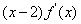 <0a="f" (
<0a="f" (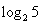 ),b="f" (
),b="f" (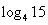 ),c="f" (
),c="f" (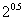 ),则a,b,c的大小关系为
),则a,b,c的大小关系为| A.a>b>c | B.c>b>a | C.b>a>c | D.c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com