
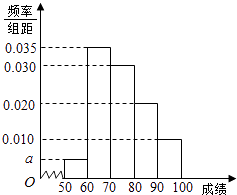
����Ŀ��ijУ100��ѧ�����п�����ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ�����гɼ������������£�
��� | ��һ�� | �ڶ��� | ������ | ������ | ������ |
���� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
������ͼ��a��ֵ��
������Ƶ�ʷֲ�ֱ��ͼ��������100��ѧ�����п�����ѧ�ɼ���ƽ���֣�
�������÷ֲ�����ķ����ӵ�3��4��5���������ȡ6��ѧ����������������һ�����壬���������ȡ2����������ǡ��1�˵ķ���������90�ֵĸ��ʣ�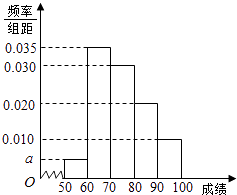
���𰸡��⣺�����������10a+0.01��10+0.02��10+0.03��10+0.035��10=1������a=0.005�� ������ֱ��ͼ������[50��60]��Ƶ��Ϊ0.05��[60��70]��Ƶ��Ϊ0.35��[70��80]��Ƶ��Ϊ0.30��
[80��90]��Ƶ��Ϊ0.20��[90��100]��Ƶ��Ϊ0.10��������100��ѧ�����п�����ѧ�ɼ���ƽ���ֵĹ���ֵΪ��55��0.05+65��0.35+75��0.30+85��0.20+95��0.10=74.5
������ֱ��ͼ���ã�
��3������Ϊ0.3��100=30��
��4������Ϊ0.2��100=20�ˣ�
��5������Ϊ0.1��100=10�ˣ�
�������÷ֲ������60��ѧ���г�ȡ6��ѧ����
ÿ��ֱ�Ϊ��
��3�飺 ![]() �ˣ�
�ˣ�
��4�飺 ![]() �ˣ�
�ˣ�
��5�飺 ![]() =1�ˣ�
=1�ˣ�
���Ե�3��4��5��ֱ��ȡ3�ˡ�2�ˡ�1�ˣ�
���3���3λͬѧΪA1 �� A2 �� A3 �� ��4���2λͬѧΪB1 �� B2 �� ��5���1λͬѧΪC1 �� �����λͬѧ�г���λͬѧ��15�ֿ������£�
��A1 �� A2������A1 �� A3������B1 �� B2������A2 �� A3������A1 �� B1������A1 �� B2������A2 �� B1������A2 �� B2������A3 �� B1������A3 �� B2������A1 �� C1������A2 �� C1������A3 �� C1������B1 �� C1������B2 �� C1����
����ǡ��1�˵ķ���������90���֣��������У���A1 �� C1������A2 �� C1������A3 �� C1������B1 �� C1������B2 �� C1������5�֣�
�������е�4���2λͬѧ������һλͬѧ��ѡ�ĸ���Ϊ ![]()
����������1���������Ը��ʵĺ�Ϊ1����������ε������Ϊ1��������ʽ��ϵ�����������2����ֵΪ��������ֵ�����Ƶ��֮���ĺͣ���3���ȷֱ����3��4��5��������������ùŵ����֪ʶ��⣮


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д� ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD��ƽ���ı��Σ�PA�͵���ABCD��AB��AC��AB=1��BC=2��PA= ![]() ��EΪBC���е㣮
��EΪBC���е㣮 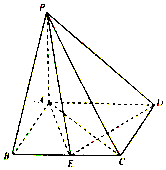
��1��֤����PE��ED��
��2��������E��PD��A�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B���صľ�����120km������ͨ����涨��A��B����֮��Ĺ�·����Ӧ������50��100km/h���������͵ļ۸���6Ԫ/������xkm/h�ٶ���ʻʱ�������ĺ�����Ϊ ![]() ��˾��ÿСʱ�Ĺ�����36Ԫ����ô��õij����Ƕ��٣�����������������ã�����г����ܷ����Ƕ��٣�
��˾��ÿСʱ�Ĺ�����36Ԫ����ô��õij����Ƕ��٣�����������������ã�����г����ܷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ϵĺ���
�ϵĺ���![]() ������
������![]() ��������
��������![]() ���������
���������![]() ����
����![]() �����ij�Ҫ�����ǣ� ��
�����ij�Ҫ�����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��������ֵ��
��������ֵ��![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ������
������![]() ���������
���������![]() �����ֵΪ
�����ֵΪ![]() ��֤����
��֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2cos2��x+2sin��xcos��x���أ�0������С������Ϊ�У�
��1����f�� ![]() ����ֵ��
����ֵ��
��2������f��x���ĵ����������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ����������������ԭ��Ϊ���㣬
Ϊ����������������ԭ��Ϊ���㣬 ![]() ��������Ϊ����ļ������У�����
��������Ϊ����ļ������У�����![]() ��
��
������ֱ��![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
����������![]() �ϵĵ㵽ֱ��
�ϵĵ㵽ֱ��![]() �ľ�������ֵ��
�ľ�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���β���ʽ��x2+x+2��0�Ľ⼯�ǣ� ��
A.{x|x����1��x��2}
B.{x|x����2��x��1}
C.{x|��1��x��2}
D.{x|��2��x��1}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͥ��������Ͷ�ʣ����ݳ����������г������Ԥ�⣬Ͷ��ծȯ���ȼ��Ͳ�ƷA��������Ͷ�ʳ����ȣ����ϵ��ͼ1��ʾ��Ͷ�ʹ�Ʊ�ȷ����Ͳ�ƷB��������Ͷ�ʵ�����ƽ���������ȣ����ϵ��ͼ2��ʾ��������Ͷ�ʵ�λ����Ԫ���� 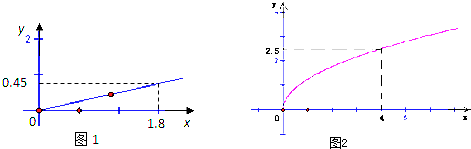
��1���ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʵĺ�����ϵʽ��
��2���ü�ͥ����10��Ԫ�ʽ𣬲�ȫ��Ͷ��ծȯ���ȼ��Ͳ�ƷA����Ʊ�ȷ����Ͳ�ƷB���ֲ�Ʒ���ʣ�����������10��ԪͶ�ʣ�����ʹͶ�ʻ��������棬���������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com