
已知函数f(x)=ax2-(2a+1)x+2lnx(a为正数).
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间;
(3)设g(x)=x2-2x,若对任意x1Î(0,2],均存在x2Î(0,2],使得f(x1)<g(x2),求实数a的取值范围.
略
【解析】f ′(x)=ax-(2a+1)+(x>0).
(1)f ′(1)=f ′(3),解得a=. ……………………4分
(2)f ′(x)=(x>0).
①当0<a<时,>2,
在区间(0,2)和(,+∞)上,f ′(x)>0;在区间(2,)上f ′(x)<0,
故f(x)的单调递增区间是(0,2)和(,+∞),单调递减区间是(2,). ……6分
②当a=时,f ′(x)=≥0,故f(x)的单调递增区间是(0,+∞). ………8分
③当a>时,0<<2,在区间(0,)和(2,+∞)上,f ′(x)>0;在区间(,2)上f ′(x)<0,故f(x)的单调递增区间是(0,)和(2,+∞),单调递减区间是(,2). …10分
(3)由已知,在(0,2]上有f(x)max<g(x)max. …………………11分
由已知,g(x)max=0,由(2)可知,
①当0<a≤时,f(x)在(0,2]上单调递增,
故f(x)max=f(2)=2a-2(2a+1)+2ln2=-2a-2+2ln2,
∴-2a-2+2ln2<0,解得a>ln2-1,ln2-1<0,故0<a≤. ……13分
②当a>时,f(x)在(0,]上单调递增,在[,2]上单调递减,
故f(x)max=f()=-2--2lna.
由a>可知lna>ln>ln=-1,2lna>-2,-2lna<2,
∴-2-2lna<0,f(x)max<0, ……………………………15分
综上所述,a>0. ……………………………16分


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源:2012-2013学年江西省南昌市高一5月联考数学卷(解析版) 题型:解答题
已知函数f(x)=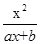 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<  .
.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁盘锦市高一第一次阶段考试数学试卷(解析版) 题型:解答题
(12分)已知函数f(x)= (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省莱芜市高三上学期10月测试理科数学 题型:解答题
(本小题满分l2分)
已知函数f(x)=a-
(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省十二校高三第一次联考数学文卷 题型:解答题
( (本小题满分13分)
已知函数f(x)=(a-1)x+aln(x-2),(a<1).
(1)讨论函数f(x)的单调性;
(2)设a<0时,对任意x1、x2∈(2,+∞),<-4恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高一期末考试文科数学 题型:解答题
(12分)已知函数f(X)=㏒a(ax-1) (a>0且a≠1 )
)
(1)求函数的定义域 (2)讨论函数f(X)的单调性
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com