练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某片森林原来面积为a，计划每年砍伐的森林面积是上一年年末森林面积的p%，当砍伐到原来面积的一半时，所用时间是10年，已知到2018年年末，森林剩余面积为原来面积的，为保护生态环境，森林面积至少要保留原来面积的.

    （1）求每年砍伐面积的百分比P%；

    （2）到2018年年末，该森林已砍伐了多少年？

    【答案】（1）每年砍伐面积的百分比p%为；（2）该森林已砍伐了5年.

    【解析】

    （1）由题意列出，解方程即可求解.

    （2）设经过m年剩余面积为原来的，可得，利用（1）结合指数的运算即可求解.

    （1）由题意可得，，

    解得，∴每年砍伐面积的百分比p%为.

    （2）设经过m年剩余面积为原来的，则，

    ∴，

    由（1）可得，即，∴，解得，

    故到2018年年末，该森林已砍伐了5年.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某煤炭公司销售人员根据该公司以往的销售情况，得到如下频率分布表

    日销售量分组

    [2,4)

    [4,6)

    [6,8)

    [8,10)

    [10,12]

    频率

    0.10

    0.20

    0.30

    0.25

    0.15

    (1)在下图中作出这些数据的频率分布直方图；

    (2)将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．若未来3天内日销售量不低于6吨的天数为X，求X的分布列、数学期望与方差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

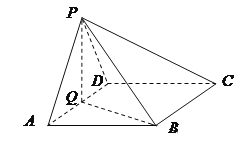
    【题目】如图，四棱锥中，底面ABCD为菱形，，Q是AD的中点.

    （Ⅰ）若，求证：平面PQB平面PAD；

    （Ⅱ）若平面APD平面ABCD，且，点M在线段PC上，试确定点M的位置，使二面角的大小为，并求出的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线的离心率为,过其右焦点作斜率为的直线，交双曲线的两条渐近线于两点（点在轴上方），则（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

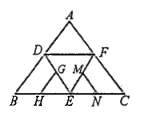
    【题目】如图是正四面体的平面展开图，分别是的中点，在这个正四面体中：①与平行；②与为异面直线；③与成60°角；④与垂直.以上四个命题中，正确命题的个数是（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量，，设函数．

    （1）若函数的图象关于直线对称，且时，求函数的单调增区间；

    （2）在（1）的条件下，当时，函数有且只有一个零点，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数的图象向左平移1个单位，再将图象上的所有点的纵坐标伸长到原来的2倍（横坐标不变），得到函数的图象．

    （1）求函数的解析式和定义域；

    （2）求函数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】表示一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系，有人根据函数图象，提出了关于这两个旅行者的如下信息：

    ①骑自行车者比骑摩托车者早出发3 h，晚到1 h；

    ②骑自行车者是变速运动，骑摩托车者是匀速运动；

    ③骑摩托车者在出发1.5 h后追上了骑自行车者；

    ④骑摩托车者在出发1.5 h后与骑自行车者速度一样．

    其中，正确信息的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2017·全国卷Ⅲ文，18)某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温(单位：℃)有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20,25)，需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

    最高气温

    [10,15)

    [15,20)

    [20,25)

    [25,30)

    [30,35)

    [35,40)

    天数

    2

    16

    36

    25

    7

    4

    以最高气温位于各区间的频率估计最高气温位于该区间的概率．

    (1)估计六月份这种酸奶一天的需求量不超过300瓶的概率；

    (2)设六月份一天销售这种酸奶的利润为Y(单位：元)．当六月份这种酸奶一天的进货量为450瓶时，写出Y的所有可能值，并估计Y大于零的概率．

    查看答案和解析>>

    同步练习册答案