根据下面一组等式:
S1=1
S2=2+3=5
S3=4+5+6=15
S4=7+8+9+10=34
S5=11+12+13+14+15=65
S6=16+17+18+19+20+21=111
可得S1+S3+S5+…+S2n-1= .
【答案】
分析:利用等差数列的通项公式与求和公式,可得S
n=(n
3+n),再以2n-1代替n,得S
2n-1=4n
3-6n
2+4n-1,结合和的特点可以求解.
解答:解:由题中数阵的排列特征,设第i行的第1个数记为a
i(i=1,2,3…n)
则a
2-a
1=1
a
3-a
2=2
a
4-a
3=3
…
a
n-a
n-1=n-1
以上n-1个式子相加可得,a
n-a
1=1+2+…+(n-1)=
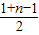
×(n-1)=

∴a
n=

+1
S
n共有n连续正整数相加,并且最小加数为
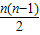
+1,最大加数

∴S
n=n•×

+

×(-1)=

(n
3+n)
∴S
2n-1=

[(2n-1)
3+(2n-1)]=4n
3-6n
2+4n-1
∴S
1=1
S1+S
3=16=2
4S
1+S
3+S
5=81=3
4∴S
1+S
3+…+S
2n-1=1+15+65+…+4n
3-6n
2+4n-1
=n
4.
故答案:n
4点评:本题以一个三角形数阵为载体,考查了等差数列的通项与求和公式、简单的合情推理等知识,属于中档题.

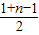 ×(n-1)=
×(n-1)=
 +1
+1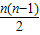 +1,最大加数
+1,最大加数 
 +
+ ×(-1)=
×(-1)= (n3+n)
(n3+n) [(2n-1)3+(2n-1)]=4n3-6n2+4n-1
[(2n-1)3+(2n-1)]=4n3-6n2+4n-1

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案