
【题目】某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为![]() ,山区边界曲线为
,山区边界曲线为![]() .计划修建的公路为
.计划修建的公路为![]() ,如图所示,
,如图所示,![]() 为
为![]() 的两个端点,测得点
的两个端点,测得点![]() 到
到![]() 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点![]() 到
到![]() 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以![]() 所在直线分别为
所在直线分别为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() .假设曲线
.假设曲线![]() 符合函数
符合函数![]() (其中
(其中![]() 为常数)模型.
为常数)模型.
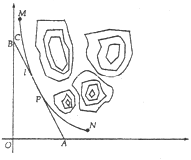
(1)求![]() 的值;
的值;
(2)设公路![]() 与曲线
与曲线![]() 相切于
相切于![]() 点,
点,![]() 的横坐标为
的横坐标为![]() .
.
①请写出公路![]() 长度的函数解析式
长度的函数解析式![]() ,并写出其定义域;
,并写出其定义域;
②当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度.
的长度最短?求出最短长度.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了解某校学生的视力情况,现采用随机抽样的方式从该校的![]() 两班中各抽5名学生进行视力检测,检测的数据如下:
两班中各抽5名学生进行视力检测,检测的数据如下:
![]() 班5名学生的视力检测结果是:
班5名学生的视力检测结果是:![]() .
.
![]() 班5名学生的视力检测结果是:
班5名学生的视力检测结果是:![]() .
.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?并计算![]() 班的5名学生视力的方差;
班的5名学生视力的方差;
(2)现从![]() 班上述5名学生中随机选取2名,求这2名学生中至少有1名学生的视力低于
班上述5名学生中随机选取2名,求这2名学生中至少有1名学生的视力低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.

(Ⅰ)求该校高三毕业班想参军的学生人数;
(Ⅱ)以这所学校的样本数据来估计全省的总体数据,若从全省高三毕业班想参军的同学中(人数很多)任选三人,设![]() 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162 ![]() (版心是指图中的长方形阴影部分,
(版心是指图中的长方形阴影部分,![]() 为长度单位分米),上、下两边各空2
为长度单位分米),上、下两边各空2 ![]() ,左、右两边各空1
,左、右两边各空1 ![]() .
.

(Ⅰ)若设版心的高为![]()
![]() ,求海报四周空白面积关于
,求海报四周空白面积关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(Ⅱ)要使海报四周空白面积最小,版心的高和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lg(ax2+2x+1) .
(1)若函数f (x)的定义域为R,求实数a的取值范围;
(2)若函数f (x)的值域为R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() ,
, ![]() ,
, ![]() 上,则在下列命题中,错误的是( )
上,则在下列命题中,错误的是( )
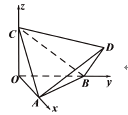
A. ![]() 是正三棱锥
是正三棱锥
B. 直线![]() 与平面
与平面![]() 相交
相交
C. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
D. 异面直线![]() 和
和![]() 所成角是
所成角是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】迭代法是用于求方程或方程组近似根的一种常用的算法设计方法.设方程为![]() ,用某种数学方法到处等价的形式
,用某种数学方法到处等价的形式![]() ,然后按以下步骤执行:
,然后按以下步骤执行:
(1)选一个方程的近似根,赋给变量![]() ;
;
(2)将![]() 的值保存于变量
的值保存于变量![]() ,然后计算
,然后计算![]() ,并将结果存于变量
,并将结果存于变量![]() ;
;
(3)当![]() 与
与![]() 的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的
的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的![]() 就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com