
ЁОЬтФПЁПдЊЕЉЦкМфЃЌФГНЮГЕЯњЪлЩЬЮЊСЫДйЯњЃЌИјГіСЫСНжжгХЛнЗНАИЃЌЙЫПЭжЛФмбЁдёЦфжаЕФвЛжжЃЌЗНАИвЛЃКУПТњ![]() ЭђдЊЃЌПЩМѕ
ЭђдЊЃЌПЩМѕ![]() ЧЇдЊЃЛЗНАИЖўЃКН№ЖюГЌЙ§
ЧЇдЊЃЛЗНАИЖўЃКН№ЖюГЌЙ§![]() ЭђдЊЃЈКЌ
ЭђдЊЃЈКЌ![]() ЭђдЊЃЉЃЌПЩвЁКХШ§ДЮЃЌЦфЙцдђЪЧвРДЮзАга
ЭђдЊЃЉЃЌПЩвЁКХШ§ДЮЃЌЦфЙцдђЪЧвРДЮзАга![]() ИіавдЫКХЁЂ
ИіавдЫКХЁЂ![]() ИіМЊЯщКХЕФвЛИівЁКХЛњЃЌзАга
ИіМЊЯщКХЕФвЛИівЁКХЛњЃЌзАга![]() ИіавдЫКХЁЂ
ИіавдЫКХЁЂ![]() ИіМЊЯщКХЕФЖўКХвЁКХЛњЃЌзАга
ИіМЊЯщКХЕФЖўКХвЁКХЛњЃЌзАга![]() ИіавдЫКХЁЂ
ИіавдЫКХЁЂ![]() ИіМЊЯщКХЕФШ§КХвЁКХЛњИївЁКХвЛДЮЃЌЦфгХЛнЧщПіЮЊЃКШєвЁГі
ИіМЊЯщКХЕФШ§КХвЁКХЛњИївЁКХвЛДЮЃЌЦфгХЛнЧщПіЮЊЃКШєвЁГі![]() ИіавдЫКХдђДђ
ИіавдЫКХдђДђ![]() елЃЌШєвЁГі
елЃЌШєвЁГі![]() ИіавдЫКХдђДђ
ИіавдЫКХдђДђ![]() елЃЛШєвЁГі
елЃЛШєвЁГі![]() ИіавдЫКХдђДђ
ИіавдЫКХдђДђ![]() елЃЛШєУЛгавЁГіавдЫКХдђВЛДђелЃЎ
елЃЛШєУЛгавЁГіавдЫКХдђВЛДђелЃЎ
ЃЈ1ЃЉШєФГаЭКХЕФГЕе§КУ![]() ЭђдЊЃЌСНИіЙЫПЭЖМбЁжаЕкЖўжаЗНАИЃЌЧѓжСЩйгавЛУћЙЫПЭБШбЁдёЗНАИвЛИќгХЛнЕФИХТЪЃЛ
ЭђдЊЃЌСНИіЙЫПЭЖМбЁжаЕкЖўжаЗНАИЃЌЧѓжСЩйгавЛУћЙЫПЭБШбЁдёЗНАИвЛИќгХЛнЕФИХТЪЃЛ
ЃЈ2ЃЉШєФуЦРгХПДжавЛПюМлИёЮЊ![]() ЭђЕФБуаЭНЮГЕЃЌЧыгУЫљбЇжЊЪЖАяжњФуХѓгбЗжЮівЛЯТгІбЁдёФФжжИЖПюЗНАИЃЎ
ЭђЕФБуаЭНЮГЕЃЌЧыгУЫљбЇжЊЪЖАяжњФуХѓгбЗжЮівЛЯТгІбЁдёФФжжИЖПюЗНАИЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉбЁдёЕкЖўжжЗНАИИљЛЎЫу
ЃЈ2ЃЉбЁдёЕкЖўжжЗНАИИљЛЎЫу
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЬѕМўПЩЕУШєбЁдёЗНАИЖўгХЛнЃЌМДжСЩйгавЛДЮУўГіЕФЪЧавдЫЧђЃЌЦфЖдСЂЪТМўЪЧШ§ДЮЖМУЛгаУўГіавдЫЧђЃЌЦфИХТЪЮЊ![]() ЃЌФЧУДСНИіШЫжСЩйгавЛИіШЫбЁдёЗНАИЖўгХЛнЕФИХТЪЮЊ
ЃЌФЧУДСНИіШЫжСЩйгавЛИіШЫбЁдёЗНАИЖўгХЛнЕФИХТЪЮЊ![]() ЃЛЃЈ2ЃЉбЁдёЗНАИвЛЕФМлИёЮЊ
ЃЛЃЈ2ЃЉбЁдёЗНАИвЛЕФМлИёЮЊ![]() ЃЈЭђдЊЃЉЃЌбЁдёЗНАИЖўЃЌЯШСаГіИЖПюН№Жю
ЃЈЭђдЊЃЉЃЌбЁдёЗНАИЖўЃЌЯШСаГіИЖПюН№Жю![]() ЕФЗжВМСаЃЌЧѓ
ЕФЗжВМСаЃЌЧѓ![]() ЕФЦкЭћЃЌШЛКѓдйБШНЯ.
ЕФЦкЭћЃЌШЛКѓдйБШНЯ.
ЪдЬтНтЮіЃКЃЈ1ЃЉбЁдёЗНАИЖўЗНАИвЛИќгХЛнЃЌдђашвЊжСЩйУўГівЛИіавдЫЧђЃЌЩшЙЫПЭВЛДђелМДШ§ДЮУЛУўГіавдЫЧђЮЊЪТМў![]() ЃЌдђ
ЃЌдђ![]() ЃЌЙЪЫљЧѓИХТЪ
ЃЌЙЪЫљЧѓИХТЪ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШєбЁдёЗНАИвЛЃЌдђашИЖПю![]() ЃЈЭђдЊЃЉЃЎ
ЃЈЭђдЊЃЉЃЎ
ШєбЁдёЗНАИЖўЃЌЩшИЖПюН№ЖюЮЊ![]() ЭђдЊЃЌдђ
ЭђдЊЃЌдђ![]() ПЩФмЕФШЁжЕЮЊ
ПЩФмЕФШЁжЕЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
ЙЪ![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 6 | 7 | 8 | 10 |
|
|
|
|
|
Ыљвд![]() ЃЈЭђдЊЃЉ
ЃЈЭђдЊЃЉ![]() ЃЈЭђдЊЃЉЃЌ
ЃЈЭђдЊЃЉЃЌ
ЫљвдбЁдёЕкЖўжжЗНАИИљЛЎЫуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ ![]() .
.
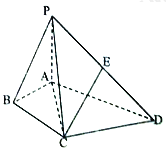
(1)ЩшЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЧѓжЄЃК
ЕФжаЕуЃЌЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
(2)ЯпЖЮ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙЕУжБЯп
ЃЌЪЙЕУжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩЕФНЧ
ЫљГЩЕФНЧ![]() ЕФе§ЯвжЕЮЊ
ЕФе§ЯвжЕЮЊ![]() ЃПШєДцдкЃЌЪдШЗЖЈЕу
ЃПШєДцдкЃЌЪдШЗЖЈЕу![]() ЕФЮЛжУЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЮЛжУЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЪ§Са{an}ЃЌa1=1ЃЌan+1= ![]() +
+ ![]() ЃЌЪ§Са{bn}ЃЌbn=2nЉ1an ЃЎ
ЃЌЪ§Са{bn}ЃЌbn=2nЉ1an ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЪ§Са{bn}ЮЊЕШВюЪ§СаЃЌВЂЧѓГі{bn}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЪ§Са{an}ЕФЧАnЯюКЭЮЊSn ЃЌ ЧѓSnЃЛ
ЃЈ3ЃЉе§Ъ§Ъ§Са{dn}Тњзу ![]() =
= ![]() ЃЎЩшЪ§Са{dn}ЕФЧАnЯюКЭЮЊDn ЃЌ ЧѓВЛГЌЙ§D100ЕФзюДѓећЪ§ЕФжЕЃЎ
ЃЎЩшЪ§Са{dn}ЕФЧАnЯюКЭЮЊDn ЃЌ ЧѓВЛГЌЙ§D100ЕФзюДѓећЪ§ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=AsinЃЈІиx+ІеЃЉЃЈAЃО0ЃЌІиЃО0ЃЌ|Іе|ЃМ ![]() ЃЉЕФзюаЁе§жмЦкЪЧ
ЃЉЕФзюаЁе§жмЦкЪЧ ![]() ЃЌзюаЁжЕЪЧЉ2ЃЌЧвЭМЯѓОЙ§ЕуЃЈ
ЃЌзюаЁжЕЪЧЉ2ЃЌЧвЭМЯѓОЙ§ЕуЃЈ ![]() ЃЌ0ЃЉЃЌдђfЃЈ0ЃЉ= ЃЎ
ЃЌ0ЃЉЃЌдђfЃЈ0ЃЉ= ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКвдЕу![]() ЮЊдВаФЕФдВгыxжсНЛгкЕуOЃЌAЃЌгыyжсНЛгкЕуOЃЌBЃЌЦфжаOЮЊдЕуЃЎ
ЮЊдВаФЕФдВгыxжсНЛгкЕуOЃЌAЃЌгыyжсНЛгкЕуOЃЌBЃЌЦфжаOЮЊдЕуЃЎ
(1)ЧѓжЄЃКЁїOABЕФУцЛ§ЮЊЖЈжЕЃЛ (2)ЩшжБЯпyЃНЃ2xЃЋ4гыдВCНЛгкЕуMЃЌNЃЌШє|OM|ЃН|ON|ЃЌЧѓдВCЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВCОЙ§ЕуAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ2ЃЉЃЌЧвдВаФCдкжБЯпy=xЩЯЃЌгжжБЯпlЃКy=kx+1гыдВCЯрНЛгкPЁЂQСНЕуЃЎ
ЃЈ1ЃЉЧѓдВCЕФЗНГЬЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓЪЕЪ§kЕФжЕЃЛ
ЃЌЧѓЪЕЪ§kЕФжЕЃЛ
ЃЈ3ЃЉЙ§ЕуЃЈ0ЃЌ4ЃЉзїЖЏжБЯпmНЛдВCгкEЃЌFСНЕуЃЎЪдЮЪЃКдквдEFЮЊжБОЖЕФЫљгадВжаЃЌЪЧЗёДцдкетбљЕФдВPЃЌЪЙЕУдВPОЙ§ЕуMЃЈ2ЃЌ0ЃЉЃПШєДцдкЃЌЧѓГідВPЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊУќЬтpЃКx2+mx+1=0гаСНИіВЛЕШЕФИКИљЃЛУќЬтqЃК4x2+4ЃЈmЉ2ЃЉx+1=0ЮоЪЕИљЃЎШєУќЬтpгыУќЬтqгаЧвжЛгавЛИіЮЊецЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮЊСЫВтСПе§дкКЃУцдШЫйааЪЛЕФФГДЌЕФЫйЖШЃЌдкКЃАЖЩЯбЁШЁОрРы1ЧЇУзЕФСНИіЙлВь
ЕуCЁЂDЃЌдкФГЬь10ЃК00ЙлВьЕНИУДЌдкAДІЃЌДЫЪБВтЕУЁЯADC=30ЁуЃЌ2ЗжжгКѓИУДЌааЪЛжСBДІЃЌДЫЪБВтЕУЁЯACB=60ЁуЃЌЁЯBCD=45ЁуЃЌЁЯADB=60ЁуЃЌ
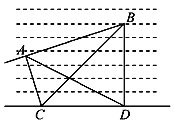
ЧѓИУДЌКНааЕФЫйЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=AsinЃЈwx+ІеЃЉЃЈxЁЪRЃЌwЃО0ЃЌ0ЃМІеЃМ ![]() ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЎ
ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЎ 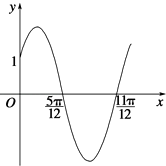
ЃЈ1ЃЉЧѓКЏЪ§fЃЈxЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓКЏЪ§gЃЈxЃЉ=fЃЈxЉ ![]() ЃЉЉfЃЈx+
ЃЉЉfЃЈx+ ![]() ЃЉЕФЕЅЕїЕндіЧјМфЃЎ
ЃЉЕФЕЅЕїЕндіЧјМфЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com