
【题目】为振兴旅游业,香港计划向内陆地区发行总量为2000万张的紫荆卡,其中向内陆人士(广东户籍除外)发行的是紫荆金卡(简称金卡),向广东籍人士发行的是紫荆银卡(简称银卡).某旅游公司组织了一个有36名内陆游客的旅游团到香港名胜旅游,其中![]() 是非广东籍内陆游客,其余是广东籍游客.在非广东新游客中有
是非广东籍内陆游客,其余是广东籍游客.在非广东新游客中有![]() 持金卡,在广东籍游客中有
持金卡,在广东籍游客中有![]() 持银卡.
持银卡.
(Ⅰ)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(Ⅱ)在该团的广东籍游客中随机采访3名游客,设其中持银卡人数为随机变量![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(Ⅰ)由题意得,境外游客有27人,其中9人持金卡;境内游客有9人,其中6人持银卡.记出事件,表示出事件的概率,根据互斥事件的概率公式,得到结论;(Ⅱ)ξ的可能取值为0,1,2,3,分别求出其对应的概率,能得到ξ的分布列和数学期望Eξ.
解析:
(Ⅰ)由题意得,非广东籍游客有27人,其中9人持金卡:广东籍游客有9人,其中6人持银卡,设事件![]() 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件![]() 为“采访该团3人中,1人持金卡,0人持银卡”,
为“采访该团3人中,1人持金卡,0人持银卡”,
事件![]() 为“采访该团3人中,1人持金卡,1人持银卡”.
为“采访该团3人中,1人持金卡,1人持银卡”.
![]() ,
,
所以在该团中随机来访3人,恰有1人持金卡且持银卡者少于2人的概率是![]() .
.
(Ⅱ)![]() 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率为80%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4,5,6,7,8表示命中,9,0表示未命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
据此估计,该运动员三次投篮均命中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对某小区30位居民的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的,饮食以肉类为主).

(1)根据茎叶图,说明这30位居民中50岁以上的人的饮食习惯;
(2)根据以上数据完成如下2×2列联表;
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(3)能否有99%的把握认为居民的饮食习惯与年龄有关?
独立性检验的临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】墙上有一壁画,最高点![]() 处离地面
处离地面![]() 米,最低点
米,最低点![]() 处离地面
处离地面![]() 米,距离墙
米,距离墙![]() 米处设有防护栏,观察者从离地面高
米处设有防护栏,观察者从离地面高![]() 米的
米的![]() 处观赏它.
处观赏它.
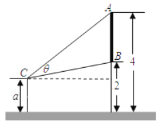
(1)当![]() 时,观察者离墙多远时,视角
时,观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() ,视角
,视角![]() 的正切值恒为
的正切值恒为![]() ,观察者离墙的距离应在什么范围内?
,观察者离墙的距离应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足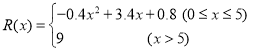 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,完成下列问题:
(1)写出利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)甲厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com