
【题目】若数列![]() 是公差为2的等差数列,数列
是公差为2的等差数列,数列![]() 满足b1=1,b2=2,且anbn+bn=nbn+1.
满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]()
对一切n∈N*恒成立,求实数λ的取值范围.
【答案】(1)![]() ;(2)(-2,3)。
;(2)(-2,3)。
【解析】
(1)对于anbn+bn=nbn+1.令n=1可求得a1=1,由等差数列的通项公式可求得an=2n-1。进而anbn+bn=nbn+1可变为2bn=bn+1,可得数列![]() 为等比数列,由等比数列的通项公式可求得bn=2n-1. (2)根据已知条件应先求得cn=
为等比数列,由等比数列的通项公式可求得bn=2n-1. (2)根据已知条件应先求得cn=![]() =
=![]() ,由特点根据错位相减法可求得Tn=4-
,由特点根据错位相减法可求得Tn=4-![]() .则不等式(-1)nλ<Tn+
.则不等式(-1)nλ<Tn+![]() ,化为(-1)nλ<4-
,化为(-1)nλ<4-![]() ,对n分奇数、偶数讨论,根据不等式恒成立可求实数λ的取值范围。
,对n分奇数、偶数讨论,根据不等式恒成立可求实数λ的取值范围。
(1) ∵数列{bn}满足b1=1,b2=2,且anbn+bn=nbn+1.
∴ n=1时,a1+1=2,解得a1=1.
又数列{an}是公差为2的等差数列,
∴an=1+2(n-1)=2n-1.
∴ 2nbn=nbn+1,化为2bn=bn+1,
∴数列{bn}是首项为1,公比为2的等比数列.
∴bn=2n-1.
(2)由数列{cn}满足cn=![]() =
=![]() =
=![]() ,数列{cn}的前n项和为
,数列{cn}的前n项和为
Tn=1+![]() +
+![]() +…+
+…+![]() ,
,
∴ ![]() Tn=
Tn=![]() +
+![]() +…+
+…+![]() +
+![]() ,
,
两式作差,得
∴![]() Tn=1+
Tn=1+![]() +
+![]() +…+
+…+![]() -
-![]() =
=![]() -
-![]() =2-
=2-![]() ,
,
∴Tn=4-![]() .
.
不等式(-1)nλ<Tn+![]() ,化为(-1)nλ<4-
,化为(-1)nλ<4-![]() ,
,
当n=2k(k∈N*)时,λ<4-![]() ,取n=2,
,取n=2,
∴λ<3.
当n=2k-1(k∈N*)时,-λ<4-![]() ,取n=1,
,取n=1,
∴λ>-2.
综上可得:实数λ的取值范围是(-2,3).


科目:高中数学 来源: 题型:
【题目】已知f(x)=xex , g(x)=﹣(x+1)2+a,若x1 , x2∈[﹣2,0],使得f(x2)≤g(x1)成立,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC,SA交于点D,E,F,H.且D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三种说法:
①命题p:x0∈R,tan x0=1,命题q:x∈R,x2-x+1>0,则命题“p∧(![]() )”是假命题.
)”是假命题.
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是![]() =-3.
=-3.
③命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”.
其中所有正确说法的序号为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在![]() 内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的编号为1,2,3,4的球,从袋中随机抽取一个球,将其编号记为m,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为n,则关于x的一元二次方程![]() 无实根的概率为__________。
无实根的概率为__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,![]() )表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.

(1)根据直方图估计这个开学季内市场需求量x的平均数和众数;
(2)将y表示为x的函数;
(3)根据频率分布直方图估计利润y不少于1050元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱A1B1C1﹣ABC中,侧棱与底面垂直,AB=BC=AA1 , ∠ABC=90°,M是BC的中点.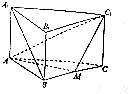
(1)求证:A1B∥平面AMC1;
(2)求平面A1B1M与平面AMC1所成角的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com