练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了让居民了解垃圾分类，养成垃圾分类的习惯，让绿色环保理念深入人心.某市将垃圾分为四类：可回收物，餐厨垃圾，有害垃圾和其他垃圾.某班按此四类由位同学组成四个宣传小组，其中可回收物宣传小组有位同学，其余三个宣传小组各有位同学.现从这位同学中选派人到某小区进行宣传活动，则每个宣传小组至少选派人的概率为（ ）

    A.B.C.D.

    【答案】D

    【解析】

    利用组合计数原理计算出基本事件的总数以及事件“从这位同学中选派人到某小区进行宣传活动，则每个宣传小组至少选派人”所包含的基本事件数，利用古典概型的概率公式可计算出所求事件的概率.

    某市将垃圾分为四类：可回收物、餐厨垃圾、有害垃圾和其他垃圾.

    某班按此四类由位同学组成四个宣传小组，

    其中可回收物宣传小组有位同学，其余三个宣传小组各有位同学.

    现从这位同学中选派人到某小区进行宣传活动，基本事件总数，

    每个宣传小组至少选派人包含的基本事件个数为，

    则每个宣传小组至少选派人的概率为.

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的左、右焦点分别是、，离心率，过点的直线交椭圆于、两点， 的周长为16．

    （1）求椭圆的方程；

    （2）已知为原点，圆： （）与椭圆交于、两点，点为椭圆上一动点，若直线、与轴分别交于、两点，求证： 为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】改革开放40年来，我国城市基础设施发生了巨大的变化，各种交通工具大大方便了人们的出行需求.某城市的A先生实行的是早九晚五的工作时间，上班通常乘坐公交或地铁加步行.已知从家到最近的公交站或地铁站都需步行5分钟，乘坐公交到离单位最近的公交站所需时间Z1（单位：分钟）服从正态分布N（33，42），下车后步行再到单位需要12分钟；乘坐地铁到离单位最近的地铁站所需时间Z2（单位：分钟）服从正态分布N（44，22），从地铁站步行到单位需要5分钟.现有下列说法：①若8：00出门，则乘坐公交一定不会迟到；②若8：02出门，则乘坐公交和地铁上班迟到的可能性相同；③若8：06出门，则乘坐公交比地铁上班迟到的可能性大；④若8：12出门，则乘坐地铁比公交上班迟到的可能性大.则以上说法中正确的序号是_____.

    参考数据：若Z～N（μ，σ2），则P（μ﹣σ＜Z≤μ+σ）=0.6826，P（μ﹣2σ＜Z≤μ+2σ）=0.9544，P（μ﹣3σ＜Z≤μ+3σ）=0.9974

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】镇江市长江路江边春江潮广场要设计一尊鼎型塑像（如图1），塑像总高度为12米，塑像由两部分组成，上半部分由四根垂直于水平地面的等高垂直立柱组成（立柱上凸起部分忽略不计），下半部分由正四棱台的上底面四根水平横柱和正四棱台的四根侧棱斜柱组成，如图2所示．设计要求正棱台的水平横柱长度为4米，下底面边长为8米，设斜柱与地面的所成的角为．

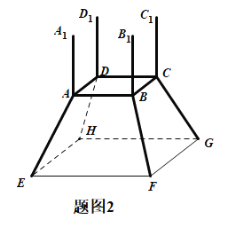
    （1）用表示塑像上半部分立柱的高度，并求的取值范围？

    （2）若该塑像上半部分立柱的造价为千元/米（立柱上凸起部分忽略不计），下半部分横柱和斜柱的造价都为2千元/米，问当为何值时，塑像总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知函数的反函数.定义：若对给定的实数，函数与互为反函数，则称满足“和性质”；若函数与互为反函数，则称满足“积性质”.

    （1） 判断函数是否满足“1和性质”，并说明理由；

    （2） 求所有满足“2和性质”的一次函数；

    （3） 设函数对任何，满足“积性质”.求的表达式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂的一台某型号机器有2种工作状态：正常状态和故障状态.若机器处于故障状态，则停机检修.为了检查机器工作状态是否正常，工厂随机统计了该机器以往正常工作状态下生产的1000个产品的质量指标值，得出如图1所示频率分布直方图.由统计结果可以认为，这种产品的质量指标值服从正态分布，其中近似为这1000个产品的质量指标值的平均数，近似为这1000个产品的质量指标值的方差（同一组中的数据用该组区间中点值为代表）.若产品的质量指标值全部在之内，就认为机器处于正常状态，否则，认为机器处于故障状态.

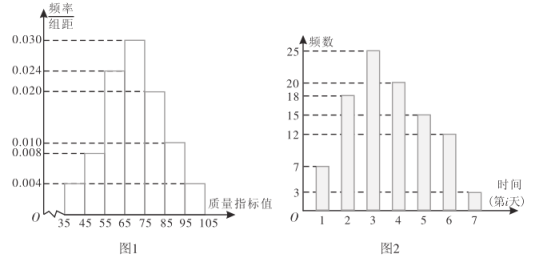
    （1）下面是检验员在一天内从该机器生产的产品中随机抽取10件测得的质量指标值：

    29 45 55 63 67 73 78 87 93 113

    请判断该机器是否出现故障？

    （2）若机器出现故障，有2种检修方案可供选择：

    方案一：加急检修，检修公司会在当天排除故障，费用为700元；

    方案二：常规检修，检修公司会在七天内的任意一天来排除故障，费用为200元.

    现需决策在机器出现故障时，该工厂选择何种方案进行检修，为此搜集检修公司对该型号机器近100单常规检修在第i（，2，…，7）天检修的单数，得到如图2所示柱状图，将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元，故障机器检修当天不工作，若机器出现故障，该选择哪种检修方案？

    附：，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是从2020年2月14日至2020年4月19日共66天的新冠肺炎中国/海外新增确诊趋势图，根据该图，下列结论中错误的是（ ）

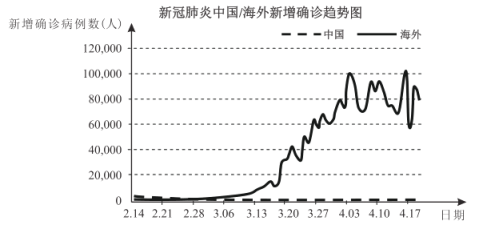
    A.从2020年2月14日起中国已经基本控制住国内的新冠肺炎疫情

    B.从2020年3月13日至2020年4月3日海外新冠肺炎疫情快速恶化

    C.这66天海外每天新增新冠肺炎确诊病例数的中位数在区间内

    D.海外新增新冠肺炎确诊病例数最多的一天突破10万例

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图．则下列说法不正确的是（ ）

    A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数

    B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果，但防控要求不能降低

    C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天

    D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位6个员工借助互联网开展工作，每个员工上网的概率都是0.5（相互独立）．至少3人同时上网的概率为________；至少________人同时上网的概率小于0.3．

    查看答案和解析>>

    同步练习册答案