
【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)试估计该年级成绩![]() 分的学生人数;
分的学生人数;
(2)已知样本中成绩在![]() 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据频数分布表,利用100名学生中![]() 的学生人所占的比例,求2000名学生中的
的学生人所占的比例,求2000名学生中的![]() 的学生人数.
的学生人数.
(2)先求从6名学生中选出2名学生的方法总数,再求一男一女的方法数,后比前即可.
试题解析:(1)100名学生中成绩![]() 的学生人数是22人,
的学生人数是22人,
所以估计年级成绩![]() 的学生人数是:
的学生人数是:![]() ;
;
(2)样本中成绩在![]() 中的6名学生中,4名男生表示为
中的6名学生中,4名男生表示为![]() ,2名女生表示为
,2名女生表示为![]() ,
,
从这6名学生中抽取两名学生有以下15种方法:
![]() ,
,
![]() ,
,
其中恰有一名男生一名女生的选取方法有8种,
所以,恰好抽到一名男生一名女生的概率是![]() .
.
点晴:本是考查的是古典概型 ,古典概型中基本事件数的常用方法有:
(1)列举法.
(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.
(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.
(4)排列组合法:适用于限制条件较多且元素数目较多的题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】重庆因夏长酷热多伏旱而得名“火炉”,八月是重庆最热、用电量最高的月份.下图是沙坪坝区居民八月份用电量(单位:度)的频率分布直方图,其分组区间依次为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中的![]() ;
;
(2)根据直方图估计八月份用电量的众数和中位数;
(3)在用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则用电量在![]() 的用户应抽取多少户?
的用户应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]()
给出下列结论:
①四面体![]() 每个面的面积相等;
每个面的面积相等;
②从四面体![]() 每个顶点出发的三条棱两两夹角之和大于
每个顶点出发的三条棱两两夹角之和大于![]() 而小于
而小于![]() ;
;
③连结四面体![]() 每组对棱中点的线段相互垂直平分;
每组对棱中点的线段相互垂直平分;
④从四面体![]() 每个顶点出发的三条棱的长可作为一个三角形的三边长;
每个顶点出发的三条棱的长可作为一个三角形的三边长;
其中正确结论的序号是__________。(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场没销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元.
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量![]() (单位:台,
(单位:台,![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量(单位:台),整理得下表:

以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,![]() 表示当周的利润(单位:元),求
表示当周的利润(单位:元),求![]() 的分布及数学期望.
的分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时
(万元);当年产量不小于80千件时![]() (万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() (
(![]() ,
,![]() )有公共焦点
)有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() ,
,![]() 在在第一象限的交点,且
在在第一象限的交点,且![]() .
.
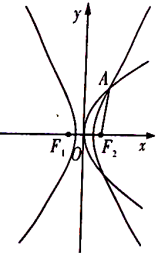
(1)求双曲线![]() 的方程;
的方程;
(2)以![]() 为圆心的圆
为圆心的圆![]() 与双曲线的一条渐进线相切,圆
与双曲线的一条渐进线相切,圆![]() .已知点
.已知点![]() ,过点
,过点![]() 作互相垂直分别与圆
作互相垂直分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 解得的弦长为
解得的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .试探索
.试探索![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:以点![]() (
(![]() )为圆心的圆与
)为圆心的圆与![]() 轴交
轴交
于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线![]() 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com