
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到椭圆上点的最远距离为3,点
,其左焦点到椭圆上点的最远距离为3,点![]() 为椭圆外一点,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分
为椭圆外一点,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分

(1)求椭圆C的标准方程
(2)求![]() 面积最大值时的直线l的方程.
面积最大值时的直线l的方程.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意![]() 都有
都有![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() ,给出如下命题:
,给出如下命题:
①![]() ;
;
②直线![]() 是函数
是函数![]() 的图象的一条对称轴;
的图象的一条对称轴;
③函数![]() 在
在![]() 上为增函数;
上为增函数;
④函数![]() 在
在![]() 上有四个零点.
上有四个零点.
其中所有正确命题的序号为( )
A. ①② B. ②④ C. ①②③ D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,O为BE中点,F为BC中点.将
,O为BE中点,F为BC中点.将![]() 沿BE折起到
沿BE折起到![]() 的位置,如图2.
的位置,如图2.
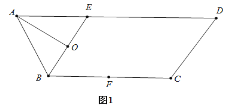
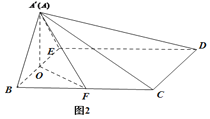
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面BCDE,求点F到平面
平面BCDE,求点F到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
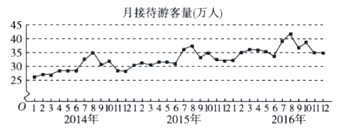
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com