
【题目】在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,且
,且![]()
![]() ,侧面
,侧面![]() 底面
底面![]() 是等边三角形.
是等边三角形.

(1)求证: ![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先取AB 中点为O,连接PO,CO,根据条件得到PO⊥AB,再结合侧面PAB⊥底面ABCD,得到PO⊥底面ABCD,即可得到OC为PC在底面ABCD上的射影;最后结合△DAB≌△OBC得BD⊥OC即可得到结论;
(2)先取PC中点E,连接BE,DE,可以证得∠BED就是二面角B-PC-D的平面角;在通过求三角形BED的三边长,即可得到结论.
试题解析:
取AB 中点为O,连接PO,CO,
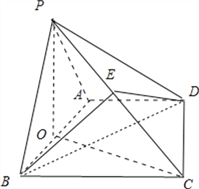
∵△PAB 是等边三角形,
∴PO⊥AB,
又∵侧面PAB⊥底面ABCD,
∴PO⊥底面ABCD,
∴OC为PC在底面ABCD上的射影,
又∵AB=BC=2AD=2,∠ABC=∠DAB=![]() ∴△DAB≌△OBC,∴∠BCO=∠DBA,
∴△DAB≌△OBC,∴∠BCO=∠DBA,
∴BD⊥OC,∴BD⊥PC.
(2)取PC中点E,连接BE,DE,
∵PB=BC,
∴BE⊥PC,
又∵BD⊥PC,BE∩BD=B,
∴PC⊥平面BDE
,∴PC⊥DE,
∴∠BED就是二面角B-PC-D的平面角.
∵AB=BC=2AD=2,∠ABC=![]() ∴BE=
∴BE=![]() PC=
PC=![]() ,PD=BD=
,PD=BD=![]() ∴DE=
∴DE=![]()
∴BE2+DE2=BD2,
∴∠BED=![]() 即二面角B-PC-D的大小为
即二面角B-PC-D的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知等式x4+a1x3+a2x2+a3x+a4=(x+1)4+b1(x+1)3+b2(x+1)2+b3(x+1)+b4,定义映射f:(a1,a2,a3,a4)→(b1,b2,b3,b4),则f(4,3,2,1)=( )
A. (1,2,3,4) B. (0,3,4,0)
C. (0,-3,4,-1) D. (-1,0,2,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为点
为点![]() 关于原点的对称点,点
关于原点的对称点,点![]() 在抛物线
在抛物线![]() 上,则下列说法错误的是( )
上,则下列说法错误的是( )
A. 使得![]() 为等腰三角形的点
为等腰三角形的点![]() 有且仅有4个
有且仅有4个
B. 使得![]() 为直角三角形的点
为直角三角形的点![]() 有且仅有4个
有且仅有4个
C. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
D. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com