【题目】如图，已知六个直角边均为1和
的直角三角形围成的两个正六边形，则该图形绕着
旋转一周得到的几何体的体积为（ ）
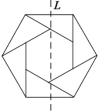
A.
B.
C.
D.
名校练考卷期末冲刺卷系列答案科目：高中数学 来源： 题型：
【题目】如图，在以
为顶点，母线长为
的圆锥中，底面圆
的直径
长为2，
是圆所在平面内一点，且
是圆的切线，连接
交圆于点
，连接
，
.
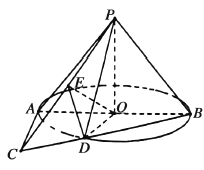
（1）求证：平面
平面
；
（2）若
是的中点，连接
，
，当二面角
的大小为
时，求平面
与平面
所成锐二面角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：如果函数
在定义域内给定区间
上存在
，满足
，则称函数是上的“平均值函数”，
是它的一个均值点．例如y=| x |是
上的“平均值函数”，0就是它的均值点．给出以下命题：
①函数
是
上的“平均值函数”．
②若是上的“平均值函数”，则它的均值点x0≥
．
③若函数
是
上的“平均值函数”，则实数m的取值范围是
．
④若
是区间[a.，b] （b>a.≥1）上的“平均值函数”，是它的一个均值点，则
．
其中的真命题有_________．（写出所有真命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足：a1＝
，an＋1＝
（n∈N*）．（其中e为自然对数的底数，e＝2.71828…）
（1）证明：an＋1>an（n∈N*）；
（2）设bn＝1－an，是否存在实数M>0，使得b1＋b2＋…＋bn≤M对任意n∈N*成立？若存在，求出M的一个值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校为了解本校文、理科学生的学业水平模拟测试数学成绩情况，分别从理科班学生中随机抽取
人的成绩得到样本甲，从文科班学生中随机抽取
人的成绩得到样本乙，根据两个样本数据分别得到如下直方图：
甲样本数据直方图
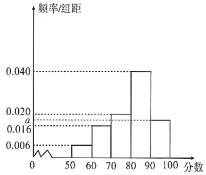
乙样本数据直方图
已知乙样本中数据在
的有
个.
（1）求和乙样本直方图中
的值；
（2）试估计该校理科班学生本次模拟测试数学成绩的平均值和文科班学生本次模拟测试数学成绩的中位数（同一组中的数据用该组区间中点值为代表）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某芯片公司为制定下一年的研发投入计划，需了解年研发资金投入量
（单位：亿元）对年销售额
（单位：亿元）的影响.该公司对历史数据进行对比分析，建立了两个函数模型:①
，②
，其中
均为常数，
为自然对数的底数．
现该公司收集了近12年的年研发资金投入量
和年销售额
的数据，
，并对这些数据作了初步处理，得到了右侧的散点图及一些统计量的值．令
，经计算得如下数据：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）设
和
的相关系数为
，
和
的相关系数为
，请从相关系数的角度，选择一个拟合程度更好的模型；
（2）（i）根据（1的选择及表中数据，建立关于的回归方程（系数精确到0.01）；
（ii）若下一年销售额需达到90亿元，预测下一年的研发资金投入量是多少亿元？
附：①相关系数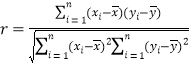
，回归直线
中斜率和截距的最小二乘估计公式分别为：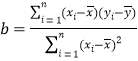
，
；
② 参考数据：
，
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年是中国改革开放的第40周年，为了充分认识新形势下改革开放的时代性，某地的民调机构随机选取了该地的100名市民进行调查，将他们的年龄分成6段：
，并绘制了如图所示的频率分布直方图.
（1）现从年龄在
内的人员中按分层抽样的方法抽取8人，再从这8人中随机抽取3人进行座谈，用
表示年龄在
内的人数，求的分布列和数学期望；
（2）若用样本的频率代替概率，用随机抽样的方法从该地抽取20名市民进行调查，其中有
名市民的年龄在
的概率为
.当
最大时，求的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
