
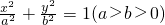 的离心率为e=
的离心率为e= ,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为
,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为 .
.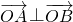 ?若存在,求出该圆的方程;若不存在说明理由.
?若存在,求出该圆的方程;若不存在说明理由. ,∴
,∴ .----------(1分)
.----------(1分) ,∴
,∴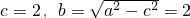 .---------------(3分)
.---------------(3分)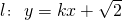 .----------(4分)
.----------(4分)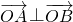 ,
, ,x1x2=
,x1x2= ,-------------------(7分)
,-------------------(7分)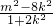
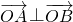 ,需使x1x2+y1y2=0,即
,需使x1x2+y1y2=0,即 ,-------------------(9分)
,-------------------(9分) -------------------(10分)
-------------------(10分)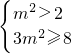 ,∴
,∴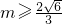 或
或 ,
,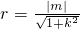 ,
, ,∴r=
,∴r=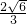 ,∴所求的圆的方程为:
,∴所求的圆的方程为: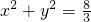 ,-------------(12分)
,-------------(12分)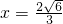 与椭圆
与椭圆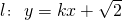 的两个交点为(
的两个交点为(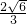 ,
,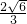 )或
)或 满足
满足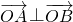 .-----------------(13分)
.-----------------(13分)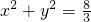 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且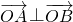 .----------------(14分)
.----------------(14分) ,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为
,点P是椭圆上的一点,且点P到椭圆E两焦点的距离之和为 ,求出几何量,从而可求椭圆E的方程;
,求出几何量,从而可求椭圆E的方程;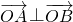 ,可确定m的范围及所求的圆的方程,验证当切线的斜率不存在时,结论也成立.
,可确定m的范围及所求的圆的方程,验证当切线的斜率不存在时,结论也成立.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
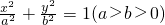 的离心率为
的离心率为 ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3. ,0)作倾角为锐角的直线l交椭圆于A,B两点,若
,0)作倾角为锐角的直线l交椭圆于A,B两点,若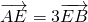 ,求l的方程.
,求l的方程.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市高二(上)期末数学试卷(解析版) 题型:解答题
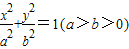 的离心率为
的离心率为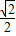 ,左焦点为F,过原点的直线l交椭圆于M,N两点,△FMN面积的最大值为1.
,左焦点为F,过原点的直线l交椭圆于M,N两点,△FMN面积的最大值为1. .
.查看答案和解析>>
科目:高中数学 来源:2008-2009学年广东省广州市越秀区育才中学高二(下)模块数学试卷(理科)(必修2+选修2-1)(解析版) 题型:解答题
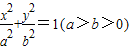 的离心率为e=
的离心率为e= ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4. ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.查看答案和解析>>
科目:高中数学 来源:2010年广东省珠海五中高考数学模拟试卷(文科)(解析版) 题型:解答题
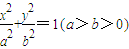 的离心率为e=
的离心率为e=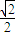 ,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.
,点A是椭圆上的一点,且点A到椭圆C两焦点的距离之和为4.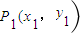 ,求3x1-4y1的取值范围.
,求3x1-4y1的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com