练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，过点作倾斜角为的直线，以原点为极点，轴非负半轴为极轴建立极坐标系，曲线的极坐标方程为，将曲线上各点的横坐标伸长为原来的2倍，纵坐标不变，得到曲线，直线与曲线交于不同的两点.

    （1）求直线的参数方程和曲线的普通方程；

    （2）求的值.

    【答案】（1）直线的参数方程为，曲线的普通方程为；（2）

    【解析】

    （1）根据直线参数方程的知识求得直线的参数方程，将的极坐标方程转化为直角坐标方程，然后通过图像变换的知识求得的普通方程.

    （2）将直线的参数方程代入曲线的普通方程，化简后写出韦达定理，根据直线参数的几何意义，求得的值.

    直线的参数方程为，

    由两边平方得，所以曲线的直角坐标方程式,

    曲线的方程为,即.

    (2)直线的参数方程为，代入曲线的方程得：

    设对应得参数分别为,则

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面为矩形，平面平面，点在线段上，且平面.

    （1）求证：平面；

    （2）若点是线段上靠近的三等分点，点在线段上，且平面，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知椭圆C：（） 经过点，设椭圆C的左顶点为A，右焦点为F，右准线于x轴交于点M，且F为线段AM的中点，

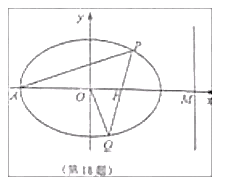
    （1）求椭圆的标准方程；

    （2）若过点A的直线l与椭圆C交于另一点P（P在x轴上方），直线PF与椭圆C相交于另一点Q，且直线l与OQ垂直，求直线PQ的斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知边长为2的正三角形ABE所在的平面与菱形ABCD所在的平面垂直，且，点F是BC上一点，且．

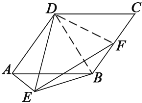
    （1）当时，证明：；

    （2）是否存在一个常数k，使得三棱锥的体积等于四棱锥的体积的，若存在，求出k的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，分别为的上、下顶点且为外的动点，且到上点的最近距离为1．

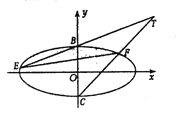
    （1）求椭圆的标准方程；

    （2）当时，设直线分别与椭圆交于两点，若的面积是的面积的倍，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”已成为当下热门的健身方式，小明的微信朋友圈内也有大量好友参与了“微信运动”，他随机选取了其中的40人（男、女各20人），记录了他们某一天的走路步数，并将数据整理如下：

    0～2000

    2001～5000

    5001～8000

    8001～10000

    男

    1

    2

    3

    6

    8

    女

    0

    2

    10

    6

    2

    （1）若采用样本估计总体的方式，试估计小明的所有微信好友中每日走路步数超过5000步的概率；

    （2）已知某人一天的走路步数超过8000步时被系统评定为“积极型”，否则为“懈怠型”.根据小明的统计完成下面的列联表，并据此判断是否有以上的把握认为“评定类型”与“性别”有关？

    积极型

    懈怠型

    总计

    男

    女

    总计

    附：

    0.10

    0.05

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，又在直角坐标系中，曲线的参数方程为（t为参数）.

    （1）求曲线的直角坐标方程和曲线的普通方程；

    （2）已知点在曲线上，点Q在曲线上，若的最小值为，求此时点的直角坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为等差数列的前项和，且，．

    （1）求数列的通项公式；

    （2）若满足不等式的正整数恰有个，求正实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中， 平面， ， ， 分别为， 的中点.

    （1）求证： 平面；

    （2）若平面平面，求直线与平面所成角的正弦值.

    查看答案和解析>>

    同步练习册答案