
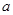 表示.已知甲、乙两个小组的数学成绩的平均分相同.
表示.已知甲、乙两个小组的数学成绩的平均分相同.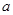 的值;
的值;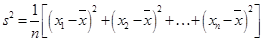 ,其中
,其中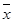 为
为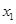 ,
,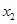 ,…,
,…, 的平均数)
的平均数)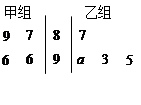
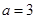 .
.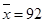 . 乙组四名同学数学成绩的方差为
. 乙组四名同学数学成绩的方差为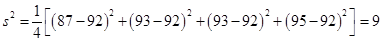 .
. 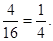
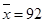 ,然后再利用方差公式计算
,然后再利用方差公式计算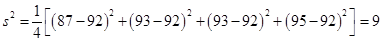 .
.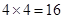 种可能的结果.然后再求出两名同学成绩之差的绝对值为3包含4种可能的结果,
种可能的结果.然后再求出两名同学成绩之差的绝对值为3包含4种可能的结果,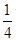 .
.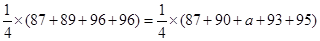 ,……2分
,……2分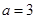 .………………………………………………………………………4分
.………………………………………………………………………4分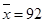 .……………………………5分
.……………………………5分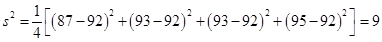 .……………8分
.……………8分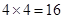 种可能的结果.
种可能的结果.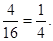 ……………………………………………………12分
……………………………………………………12分

科目:高中数学 来源:不详 题型:单选题
| A.80;8 | B.80;64 | C.70;4 | D.70;3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
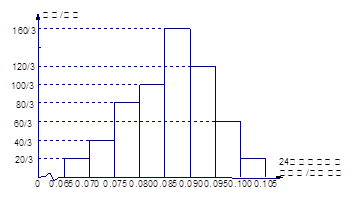
| A.2 | B.3 | C.28 | D.27 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
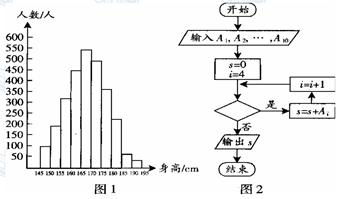
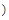 内的人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在[160,180
内的人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在[160,180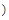 内的学生人数,那么在流程图中的判断框内应填写的条件是( )
内的学生人数,那么在流程图中的判断框内应填写的条件是( )| A.i<6 | B.i<7 | C.i<8 | D.i<9 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
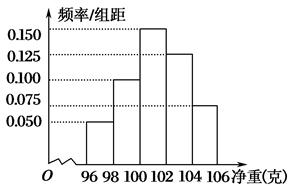
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.12人 | B.27人 | C.32人 | D.33人 |
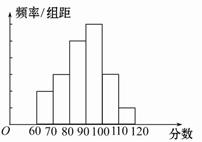
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
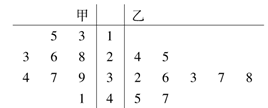
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com