练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    三个人踢球，互相传递，每人每次只能踢一次，由甲开始踢，经过5次传递后，球又被踢回给甲，则不同的传递方式共有（        ）
    A．6种B．10种C．12种 D．16种
    B
    根据题意，设在第n次传球后（n≥2），有种情况球在甲手中，即经过n次传递后，球又被传回给甲，而前n次传球中，每次传球都有2种方法，则前n次传球的不同的传球方法共有种，那么在第n次传球后，球不在甲手中的情况有种情况，即球在乙或丙手中，只有在这些情况时，在第n+1次传球后，球才会被传回甲，即；易得=2，则=-2=2，=-2=6，=-6=10，
    故选B，本题也可用树状图易得。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    甲、乙、丙三人站在共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法总数为___▲　　．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某班班会准备从甲、乙等7名学生中选派4名学生发言，要求甲、乙两人至少有一人参加．当甲乙同时参加时，他们两人的发言不能相邻．那么不同的发言顺序的种数为(　　)                                                       
    A．360B．520C．600D．720

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某成品的组装工序图如右，箭头上的数字表示组装过程中所需要的时间（小时），不同车间可同时工作，同一车间不能同时做两种或两种以上的工作，则组装该产品所需要的最短时间是（   ）
    A．11B．13C．15D．17

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

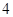    用红、黄、蓝、白、黑五种颜色在“田”字形的个小方格内，每格涂一种颜色，相邻（有公共边）两格涂不同的颜色，如果颜色可以反复使用，共有             种不同的涂色方法。             

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    五人站成一排.求下列问题的排法总数；
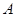    （1）不站在排头也不站在排尾；     （2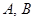）两人都不站在两端；
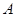    （3）不站在排头，不站在排尾；   （4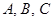）两两不相邻.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    把5名新同学分配到高一年级的A、B、C三个班，每班至少分配一人，其中甲同学已分配到A班，则其余同学的分配方法共有（  ）
    A、24种 B、50种 C、56种 D、08种

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    甲、乙、丙3人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法总数是               ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若自然数n使得作加法运算不产生进位现象，则称n为“给力数”.例如:32是 “给力数”，因为32 +33 +34不产生进位现象;23不是“给力数”，因为23 +24 +25产生进位现象.设小于1 000的所有“给力数”的各数位上的数字组成集合A，则用集合4中的数字可组成无重复数字的四位偶数的个数是________

    查看答案和解析>>

    同步练习册答案