
【题目】某班有![]() 个小组,甲、乙、丙三人分别在不同的小组.某次数学考试成绩公布情况如下:甲和三人中等第
个小组,甲、乙、丙三人分别在不同的小组.某次数学考试成绩公布情况如下:甲和三人中等第![]() 小组的那位的成绩不一样,丙比三人中第
小组的那位的成绩不一样,丙比三人中第![]() 组的那位的成绩低,三人中第
组的那位的成绩低,三人中第![]() 小组的那位比乙的成绩高.若将甲、乙、丙三人按数学成绩由高到低排列,则正确的排列顺序是______.
小组的那位比乙的成绩高.若将甲、乙、丙三人按数学成绩由高到低排列,则正确的排列顺序是______.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知![]() ,则
,则![]() ;
;
②![]() 为空间四点,若
为空间四点,若![]() 不构成空间的一个基底,那么
不构成空间的一个基底,那么![]() 共面;
共面;
③已知![]() ,则
,则![]() 与任何向量都不构成空间的一个基底;
与任何向量都不构成空间的一个基底;
④若![]() 共线,则
共线,则![]() 所在直线或者平行或者重合.
所在直线或者平行或者重合.
正确的结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有![]() 个小组,甲、乙、丙三人分别在不同的小组.某次数学考试成绩公布情况如下:甲和三人中等第
个小组,甲、乙、丙三人分别在不同的小组.某次数学考试成绩公布情况如下:甲和三人中等第![]() 小组的那位的成绩不一样,丙比三人中第
小组的那位的成绩不一样,丙比三人中第![]() 组的那位的成绩低,三人中第
组的那位的成绩低,三人中第![]() 小组的那位比乙的成绩高.若将甲、乙、丙三人按数学成绩由高到低排列,则正确的排列顺序是______.
小组的那位比乙的成绩高.若将甲、乙、丙三人按数学成绩由高到低排列,则正确的排列顺序是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
B.四棱锥的四个侧面都可以是直角三角形
C.有两个平面互相平行,其余各面都是梯形的多面体是棱台
D.棱台的各侧棱延长后不一定交于一点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某年龄段人群的午休睡眠质量,随机抽取了1000名该年龄段的人作为被调查者,统计了他们的午休睡眠时间,得到如图所示频率分布直方图.
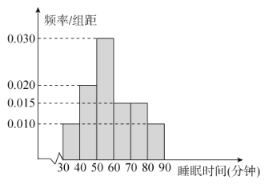
(1)求这1000名被调查者的午休平均睡眠时间![]() ;(同一组中数据用该组区间中点作代表)
;(同一组中数据用该组区间中点作代表)
(2)由直方图可以认为被调查者的午休睡眠时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() ,
,![]() 分别取被调查者的平均午休睡眠时间
分别取被调查者的平均午休睡眠时间![]() 和方差
和方差![]() ,那么这1000名被调查者中午休睡眠时间低于43.91分钟(含43.91)的人数估计有多少?
,那么这1000名被调查者中午休睡眠时间低于43.91分钟(含43.91)的人数估计有多少?
(3)如果用这1000名被调查者的午休睡眠情况来估计某市该年龄段所有人的午休睡眠情况,现从全市所有该年龄段人中随机抽取2人(午休睡眠时间不高于43.91分钟)和3人(午休睡眠时间不低于73.09分钟)进行访谈后,再从抽取的这5人中推荐3人作为代表进行总结性发言,设推荐出的代表者午休睡眠时间均不高于43.91分钟的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①![]() ,
,![]() .②
.②![]() ,则
,则![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如表数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 10 |
若用表中数据所得频率代替概率.
(1)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其他市民.现对
类是其他市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() .使得函数
.使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() 若存在,求实数
若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com