
【题目】已知数列![]() ,
,![]() ,数列
,数列![]() 满足
满足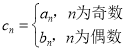 ,n
,n![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的前2n项和
的前2n项和![]() ;
;
(2)若数列![]() 为等差数列,且对任意n
为等差数列,且对任意n![]() ,
,![]() 恒成立.
恒成立.
①当数列![]() 为等差数列时,求证:数列
为等差数列时,求证:数列![]() ,
,![]() 的公差相等;
的公差相等;
②数列![]() 能否为等比数列?若能,请写出所有满足条件的数列
能否为等比数列?若能,请写出所有满足条件的数列![]() ;若不能,请说明理由.
;若不能,请说明理由.
【答案】(1)![]() (2)①见解析②数列
(2)①见解析②数列![]() 不能为等比数列,见解析
不能为等比数列,见解析
【解析】
(1)根据数列通项公式的特点,奇数项为等差数列,偶数项为等比数列,选用分组求和的方法进行求解;
(2)①设数列![]() 的公差为
的公差为![]() ,数列
,数列![]() 的公差为
的公差为![]() ,当n为奇数时,得出
,当n为奇数时,得出![]() ;当n为偶数时,得出
;当n为偶数时,得出![]() ,从而可证数列
,从而可证数列![]() ,
,![]() 的公差相等;
的公差相等;
②利用反证法,先假设![]() 可以为等比数列,结合题意得出矛盾,进而得出数列
可以为等比数列,结合题意得出矛盾,进而得出数列![]() 不能为等比数列.
不能为等比数列.
(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() 且
且![]() ,
,![]()
由题意可知,数列![]() 是以1为首项,2为公差的等差数列,
是以1为首项,2为公差的等差数列,
数列![]() 是首项和公比均为4的等比数列,
是首项和公比均为4的等比数列,
所以![]() ;
;
(2)①证明:设数列![]() 的公差为
的公差为![]() ,数列
,数列![]() 的公差为
的公差为![]() ,
,
当n为奇数时,![]() ,
,![]()
若![]() ,则当
,则当![]() 时,
时,![]() ,
,
即![]() ,与题意不符,所以
,与题意不符,所以![]() ,
,
当n为偶数时,![]() ,
,![]() ,
,
若![]() ,则当
,则当![]() 时,
时,![]() ,
,
即![]() ,与题意不符,所以
,与题意不符,所以![]() ,
,
综上,![]() ,原命题得证;
,原命题得证;
②假设![]() 可以为等比数列,设公比为q,
可以为等比数列,设公比为q,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,
因为当![]() 时,
时,
![]() ,
,
所以当n为偶数,且![]() 时,
时,![]() ,
,
即当n为偶数,且![]() 时,
时,![]() 不成立,与题意矛盾,
不成立,与题意矛盾,
所以数列![]() 不能为等比数列.
不能为等比数列.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,满足
,满足![]() .设
.设![]() 为
为![]() 上任一点,过
上任一点,过![]() 作
作![]() 的切线,其斜率
的切线,其斜率![]() 满足
满足![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若数列![]() 满足
满足![]() .设
.设![]() 为正常数.
为正常数.
①求![]() ;
;
②若不等式![]() 对任意的
对任意的![]() 恒成立,则实数
恒成立,则实数![]() 是否存在最大值?若存在,请求出这个值;若不存在,请说明理由.
是否存在最大值?若存在,请求出这个值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过点
)经过点![]() ,离心率为
,离心率为![]() ,
,![]() ,
,![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)求椭圆C的标准方程;
(2)若点![]() (
(![]() )在椭圆C上,求证;直线
)在椭圆C上,求证;直线![]() 与直线
与直线![]() 关于直线l:
关于直线l:![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足bcosA﹣![]() asinB=0.
asinB=0.
(1)求A;
(2)已知a=2![]() ,B=
,B=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据:
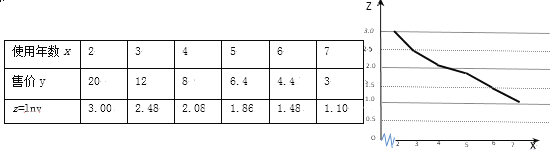
如图是z关于x的折线图:
(1)由折线图可以看出,可以用线性回归模型拟合z和x的关系,请用相关系数r加以说明(注:若相关系数︱r︱![]() 0.75,则认为两个变量相关程度较强);
0.75,则认为两个变量相关程度较强);
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?(![]() 小数点后面保留两位有效数字);
小数点后面保留两位有效数字);
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号的二手车时车辆的使用年限不得超过多少年?
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
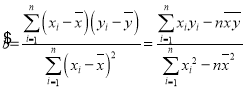 ,
,
参考数据: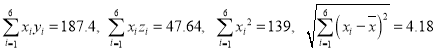
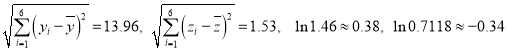
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为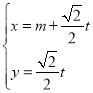 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣,“放牧人粗心大意,三畜偷偷吃苗青,苗主扣住牛马羊,要求赔偿五斗粮,三畜户主愿赔偿,牛马羊吃得异样.马吃了牛的一半,羊吃了马的一半.”请问各畜赔多少?它的大意是放牧人放牧时粗心大意,牛、马、羊偷吃青苗,青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食(1斗=10升),三畜的主人同意赔偿,但牛、马、羊吃的青苗量各不相同.马吃的青苗是牛的一半,羊吃的青苗是马的一半.问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,圆台
,圆台![]() 的侧面积为
的侧面积为![]() .若点C,D分别为圆
.若点C,D分别为圆![]() ,
,![]() 上的动点且点C,D在平面
上的动点且点C,D在平面![]() 的同侧.
的同侧.
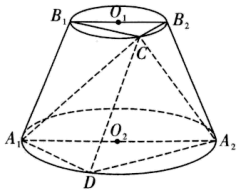
(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求多面体
的体积取最大值时,求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com