
若函数f(x)= sin2ωx-sinωxcosωx(ω>0)的图象与直线y=m (m为常数)相切,并且切点的横坐标依次成公差为![]() 的等差数列.
的等差数列.
(Ⅰ)求m的值;
(Ⅱ)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈[0,![]() ],求点A的坐标.
],求点A的坐标.
科目:高中数学 来源: 题型:
| 3 |
| AB |
| AC |
| x |
| 4 |
| x |
| 4 |
| 3 |
| x |
| 4 |
| x |
| 4 |
查看答案和解析>>
科目:高中数学 来源:镇江市2006-2007学年第一学期期中统测试卷高三数学 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
①若f(x)=![]() ,则f′(0)=0 ②若函数?f(x)=2x2+1,图象上点(1,3)的邻近一点为(1+Δx,3+Δy),则
,则f′(0)=0 ②若函数?f(x)=2x2+1,图象上点(1,3)的邻近一点为(1+Δx,3+Δy),则![]() =4+2Δx ③加速度是动点位移函数s(t)对时间t的导数 ④曲线y=x3在(0,0)处没有切线
=4+2Δx ③加速度是动点位移函数s(t)对时间t的导数 ④曲线y=x3在(0,0)处没有切线
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
. 已知函数f(x)=ax2+ax和g(x)=x-a,其中a??R且a??0.
(1)若函数f(x)与g(x)的图像的一个公共点恰好在x轴上,求![]() 的值;
的值;
(2)若函数f(x)与g(x)图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的![]() 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.
(3)若p和q是方程f(x)=g(x)的两根,且满足0<p<q<,证明:当x??(0,p)时,g(x)<f(x)<p-a..
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-2 1.1导数的概念练习卷(解析版) 题型:选择题
给出下列命题:
(1)若函数f(x)=|x|,则f’(0)=0;
(2)若函数f(x)=2x2+1,图象上P(1,3)及邻近上点Q(1+Δx,3+Δy),
则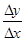 =4+2Δx
=4+2Δx
(3)加速度是动点位移函数S(t)对时间t的导数;
(4)y=2cosx+lgx,则y’=-2cosx·sinx+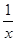
其中正确的命题有( )
A. 0个 B.1个 C.2个 D。3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com