解:(1)函数f(x)=xlnx,f′(x)=lnx+1,当x∈[1,3]时,f′(x)>0,
因此f(x)在[1,3]上为单调递增函数,所以f(x)
min=f(1)=0
(2)要求f(x),g(x)在区间[1,3]上单调性相同,而f(x)在[1,3]上为单调递增函数,所以g(x)在区间[1,3]上单调递增,因为g(x)=-x
2+2ax-3,g′(x)=-2x+2a,即g′(x)≥0当x∈[1,3]时恒成立,
所以-2x+2a≥0,因此a≥x,当x∈[1,3]时恒成立,
所以a的取值范围是[3,+∞).
(3)函数f(x)=xlnx,f′(x)=lnx+1,可知函数f(x)在(0,+∞)上的最小值为f(

)=-

,
设h(x)=
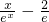
,则h′(x)=
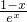
,可知函数h(x)在(0,+∞)上的最大值为h(1)=-

,所以当x∈(0,+∞)时,f(x)≥f(

)=-

=h(1)≥h(x),
综上所述,当x∈(0,+∞)时,
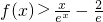
分析:(1)求出f′(x),然后在区间[1,3]上判断导函数的正负决定函数的增减性,然后得到函数的最小值即可;
(2)由(1)得到f(x)在[1,3]上为增函数,所以得到g(x)也为增函数,即得到g′(x)>0,求出a的最小值,即可得到a的取值范围;(3)在区间(0,+∝)上求出f(x)的最小值,设h(x)=
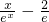
,求出导函数得到h(x)的最大值,让f(x)的最小值大于h(x)的最大值得证.
点评:考查学生会利用导数研究函数的极值及会利用导数研究函数的单调性,掌握函数恒成立时所取的条件.此题是一道综合题,要求学生掌握知识要全面.

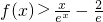 .
. )=-
)=- ,
,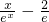 ,则h′(x)=
,则h′(x)=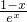 ,可知函数h(x)在(0,+∞)上的最大值为h(1)=-
,可知函数h(x)在(0,+∞)上的最大值为h(1)=- ,所以当x∈(0,+∞)时,f(x)≥f(
,所以当x∈(0,+∞)时,f(x)≥f( )=-
)=- =h(1)≥h(x),
=h(1)≥h(x),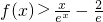
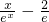 ,求出导函数得到h(x)的最大值,让f(x)的最小值大于h(x)的最大值得证.
,求出导函数得到h(x)的最大值,让f(x)的最小值大于h(x)的最大值得证.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<