
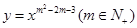 的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x-
的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x-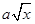 在(0,1)上为减函数.
在(0,1)上为减函数.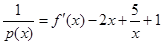 ,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足
,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足 ,
, ,求数列{an}的通项公式an和sn.
,求数列{an}的通项公式an和sn.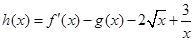 ,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.
,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由. ;②
;②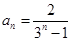 ;
;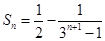 ;③见解析.
;③见解析. 的取值集合,由图像关于原点对称的函数是奇函数可以确定
的取值集合,由图像关于原点对称的函数是奇函数可以确定 的值,将
的值,将 的值代入
的值代入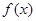 ,
,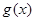 的解析式后,根据函数的单调性与导函数的关系以及不等式的恒成立问题的解法就可以知道
的解析式后,根据函数的单调性与导函数的关系以及不等式的恒成立问题的解法就可以知道 满足的不等式,就可以解得
满足的不等式,就可以解得 的值;②先由已知条件求出
的值;②先由已知条件求出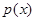 的解析式,然后得出
的解析式,然后得出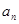 ,
,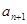 的关系,由函数构造的方法可以求得
的关系,由函数构造的方法可以求得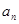 的解析式,代入
的解析式,代入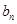 即可,再由数列求和公式求得
即可,再由数列求和公式求得 的值;③先求出
的值;③先求出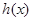 的解析式,再由相减的方法来判断两个式子的大小,最后减得的结果和0比较即可,注意分类讨论的思想.
的解析式,再由相减的方法来判断两个式子的大小,最后减得的结果和0比较即可,注意分类讨论的思想. 轴,
轴,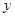 轴无交点,则有
轴无交点,则有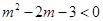 ,解得
,解得
 ,∴
,∴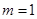 或
或 ,
,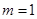 时,
时, 是偶函数,不合题意,舍去,
是偶函数,不合题意,舍去, 时,
时,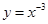 是奇函数,∴
是奇函数,∴ ,
,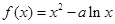 ,求导得
,求导得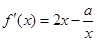 ,
,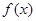 在
在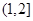 上是增函数,∴
上是增函数,∴ 在
在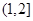 上恒成立,
上恒成立,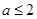 ,
, ,
,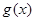 在
在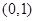 上为减函数,
上为减函数, 在
在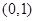 上恒成立,
上恒成立, ,
, ; ..3分
; ..3分 ,
, ∴
∴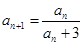 ∴
∴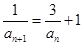 ∴
∴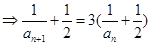 ,
, 是首项为
是首项为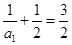 公比
公比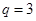 的等比数列,
的等比数列,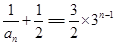 解得
解得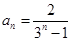 ,
,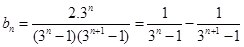 ,
,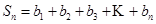 ,
,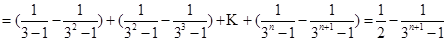 ; .6分
; .6分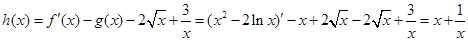 ,
,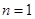 时,
时,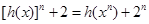 ,
,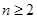 时,
时,



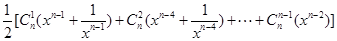
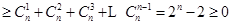 ,
,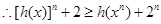 . 10分
. 10分

科目:高中数学 来源:不详 题型:解答题
 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C. 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程; 的面积的最大值。
的面积的最大值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度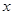 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当 时,车流速度
时,车流速度 是车流密度
是车流密度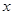 的一次函数.
的一次函数. 时,求函数
时,求函数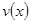 的表达式;
的表达式;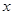 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com