解:(1)n=1时,a
1=S
1=a,
n≥2时,
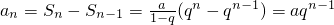
∵n=1时,a
1=a=aq
1-1也符合
∴
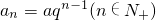
,可得
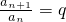
,即数列{a
n}是公比为q等比数列.
(2)设存在某一项,它能表示为另外三项之和,即
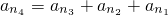
,
则
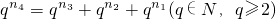
,
易得n
4是n
1、n
2、n
3、n
4中的最大值,不妨设n
4>n
3>n
2>n
1,
两边同除以
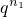
,整理得:
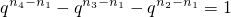
因为左边能被q整除,右边不能被q整除,因此满足条件的q不存在.
∴不存在q的某些取值,使数列{a
n}中某一项能表示为另外三项之和
(3)若
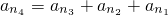
则
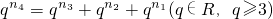
易得n
4是n
1、n
2、n
3、n
4中的最大值,不妨设n
4>n
3>n
2>n
1,
∵q≥3,

,
∴
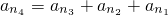
不成立.
因此,不存在q∈[3,+∞),使数列{a
n}中,某一项可以表示为另外三项之和.
分析:(1)利用公式a
n=
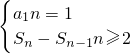
进行讨论,然后综合可得a
n的通项公式,从而证出数列{a
n}是公比为q等比数列.
(2)假设存在满足条件的一项能表示为另外三项之和,设
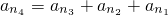
,经过讨论可变形为
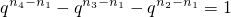
,根据等式两边对q的整除性,可知等式不成立,从而得到不存在满足条件的q值.
(3)用类似(2)的方法,设
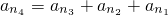
,结合{a
n}的通项公式和q≥3,利用不等式的性质证明出
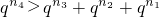
恒成立,从而证出等式不成立,从而得到不存在满足条件的q值.
点评:本题给出等比数列,要我们探索能否存在一项使它等于另外三项的和,着重考查了等比数列的通项公式和不等式的基本性质等知识,属于中档题.

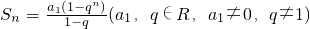 .
.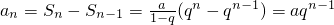
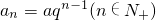 ,可得
,可得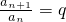 ,即数列{an}是公比为q等比数列.
,即数列{an}是公比为q等比数列.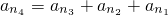 ,
,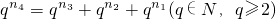 ,
,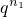 ,整理得:
,整理得: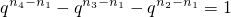
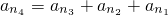 则
则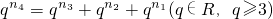
 ,
,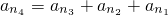 不成立.
不成立.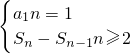 进行讨论,然后综合可得an的通项公式,从而证出数列{an}是公比为q等比数列.
进行讨论,然后综合可得an的通项公式,从而证出数列{an}是公比为q等比数列.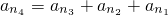 ,经过讨论可变形为
,经过讨论可变形为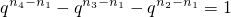 ,根据等式两边对q的整除性,可知等式不成立,从而得到不存在满足条件的q值.
,根据等式两边对q的整除性,可知等式不成立,从而得到不存在满足条件的q值.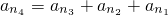 ,结合{an}的通项公式和q≥3,利用不等式的性质证明出
,结合{an}的通项公式和q≥3,利用不等式的性质证明出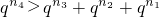 恒成立,从而证出等式不成立,从而得到不存在满足条件的q值.
恒成立,从而证出等式不成立,从而得到不存在满足条件的q值.
