
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 且斜率为
且斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点.若线段
两点.若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由题意可知:抛物线y2=2px(p>0)的焦点为F(![]() ,0),直线AB的斜率为
,0),直线AB的斜率为![]() ,则垂直平分线的斜率为﹣
,则垂直平分线的斜率为﹣![]() ,且与x轴交于点M(11,0),则y=﹣
,且与x轴交于点M(11,0),则y=﹣![]() (x﹣11),则直线AB的方程为y=
(x﹣11),则直线AB的方程为y=![]() (x﹣
(x﹣![]() ),代入抛物线方程,由韦达定理可知:x1+x2=
),代入抛物线方程,由韦达定理可知:x1+x2=![]() ,根据中点坐标公式求得中点P坐标,代入AB的垂直平分线方程,即可求得p的值.
,根据中点坐标公式求得中点P坐标,代入AB的垂直平分线方程,即可求得p的值.
由题意可知:抛物线y2=2px(p>0)的焦点为F(![]() ,0),
,0),
直线AB的斜率为![]() ,则垂直平分线的斜率为﹣
,则垂直平分线的斜率为﹣![]() ,且与x轴交于点M(11,0),则y=﹣
,且与x轴交于点M(11,0),则y=﹣![]() (x﹣11),
(x﹣11),
设直线AB的方程为:y=![]() (x﹣
(x﹣![]() ),A(x1,y1),B(x2,y2),AB的中点为P(x0,y0),
),A(x1,y1),B(x2,y2),AB的中点为P(x0,y0),
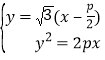 ,整理得:3x2﹣5px+
,整理得:3x2﹣5px+![]() =0,
=0,
由韦达定理可知:x1+x2=![]() ,
,
由中点坐标公式可知:x0=![]() ,则y0=
,则y0=![]() ,
,
由P在垂直平分线上,则y0=﹣![]() (x0﹣11),即p=﹣(
(x0﹣11),即p=﹣(![]() ﹣11),
﹣11),
解得:p=6,
故选:C.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 为椭圆
为椭圆![]() 上不同于点
上不同于点![]() 的点,直线
的点,直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】( 本小题满分14)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
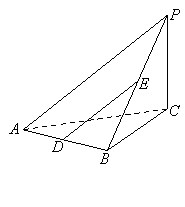
(1)求证:DE∥平面PAC
(2)求证:AB⊥PB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 经过定点
经过定点![]() ,且与直线
,且与直线![]() 相切,设动圆圆心
相切,设动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() ,
,![]() 分别与曲线
分别与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 的斜率存在,且倾斜角互补,证明:直线
的斜率存在,且倾斜角互补,证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD是边长为2的正方形,且DE=![]() ,平面ABCD⊥平面ADE,∠ADE=30°
,平面ABCD⊥平面ADE,∠ADE=30°
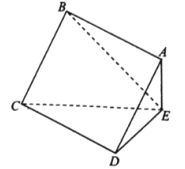
(1)求证:AE⊥平面CDE;
(2)求AB与平面BCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义实数a,b间的计算法则如下![]() .
.
(1)计算![]() ;
;
(2)对![]() 的任意实数x,y,z,判断
的任意实数x,y,z,判断![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)写出函数![]() ,
,![]() 的解析式,作出该函数的图象,并写出该函数单调递增区间和值域(只需要写出结果).
的解析式,作出该函数的图象,并写出该函数单调递增区间和值域(只需要写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com