
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右顶点为
的右顶点为![]() ,过点
,过点![]() 作直线
作直线![]() 与圆
与圆![]() 相切,与椭圆
相切,与椭圆![]() 交于另一点
交于另一点![]() ,与右准线交于点
,与右准线交于点![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
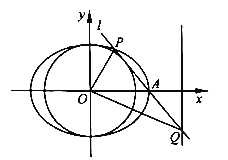
(1)用![]() 表示椭圆
表示椭圆![]() 的离心率;
的离心率;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() :
:![]() 的下列说法:①关于原点对称;②关于直线
的下列说法:①关于原点对称;②关于直线![]() 对称;③是封闭图形,面积大于
对称;③是封闭图形,面积大于![]() ;④不是封闭图形,与圆
;④不是封闭图形,与圆![]() 无公共点;⑤与曲线D:
无公共点;⑤与曲线D:![]() 的四个交点恰为正方形的四个顶点,其中正确的个数是( )
的四个交点恰为正方形的四个顶点,其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面内互不平行的三个向量,
是平面内互不平行的三个向量,![]() ,有下列命题:
,有下列命题:
①方程![]() 不可能有两个不同的实数解;
不可能有两个不同的实数解;
②方程![]() 有实数解的充要条件是
有实数解的充要条件是![]() ;
;
③方程![]() 有唯一的实数解
有唯一的实数解![]() ;
;
④方程![]() 没有实数解.
没有实数解.
其中真命题有 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形,且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵,![]() ,若
,若![]() ,当阳马
,当阳马![]() 体积最大时,则堑堵
体积最大时,则堑堵![]() 的外接球体积为( )
的外接球体积为( )
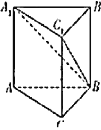
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
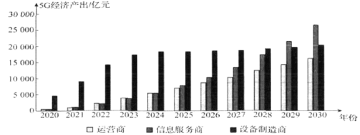
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,把长为6,宽为3的矩形折成正三棱柱![]() ,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱
,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱![]() 的交点记为E,F.
的交点记为E,F.
(1)求三棱柱![]() 的体积;
的体积;
(2)求三棱柱中异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
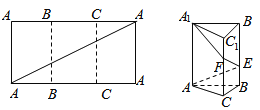
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
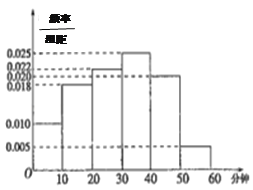
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的2×2列联表,若按95%的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)现在从该地区非体育迷的电视观众中,采用分层抽样方法选取5名观众,求从这5名观众选取两人进行访谈,被抽取的2名观众中至少有一名女生的概率.
附:![]()
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com