
设数列{bn}满足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-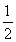 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
(1)b1=-1(2)见解析(3)
【解析】(1)∵bn+2=-bn+1-bn,
∴b3=-b2-b1=-3b1=3,
∴b1=-1;(3分)
(2)∵bn+2=-bn+1-bn①,
∴bn+3=-bn+2-bn+1②,
②-①得bn+3=bn,(5分)
∴(bn+1bn+2bn+3+n+1)-(bnbn+1bn+2+n)=bn+1bn+2(bn+3-bn)+1=1为常数,
∴数列{bnbn+1bn+2+n}是等差数列.(7分)
(3)∵Tn+1=Tn·bn+1=Tn-1bnbn+1=Tn-2bn-1bnbn+1=…=b1b2b3…bn+1
当n≥2时Tn=b1b2b2…bn(*),
当n=1时,T1=b1适合(*)式
∴Tn=b1b2b3…bn(n∈N*).(9分)
∵b1=- ,b2=2b1=-1,
,b2=2b1=-1,
b3=-3b1= ,bn+3=bn,
,bn+3=bn,
∴T1=b1=- ,T2=T1b2=
,T2=T1b2= ,
,
T3=T2b3= ,T4=T3b4=T3b1=
,T4=T3b4=T3b1= T1,
T1,
T5=T4b5=T2b3b4b5=T2b1b2b3= T2,
T2,
T6=T5b6=T3b4b5b6=T3b1b2b3= T3,
T3,
……
T3n+1+T3n+2+T3n+3=T3n-2b3n-1b3nb3n+1+
T3n-1b3nb3n+1b3n+2+T3nb3n+1b3n+2b3n+3
=T3n-2b1b2b3+T3n-1b1b2b3+T3nb1b2b3
= (T3n-2+T3n-1+T3n),
(T3n-2+T3n-1+T3n),
∴数列{T3n-2+T3n-1+T3n)(n∈N*)是等比数列,
首项T1+T2+T3= 且公比q=
且公比q= ,(11分)记Sn=T1+T2+T3+…+Tn,
,(11分)记Sn=T1+T2+T3+…+Tn,
①当n=3k(k∈N*)时,
Sn=(T1+T2+T3)+(T4+T5+T6)…+(T3k-2+T3k-1+T3k)
= ,
,
∴ ≤Sn<3;(13分)
≤Sn<3;(13分)
②当n=3k-1(k∈N*)时
Sn=(T1+T2+T3)+(T4+T5+T6)+…+(T3k-2+T3k-1+T3k)-T3k
=3 -(b1b2b3)k=3-4·
-(b1b2b3)k=3-4· ∴0≤Sn<3;(14分)
∴0≤Sn<3;(14分)
③当n=3k-2(k∈N*)时
Sn=(T1+T2+T3)+(T4+T5+T6)+…+(T3k-2+T3k-1+T3k)-T3k-1-T3k
=3 -(b1b2b3)k-1b1b2-
-(b1b2b3)k-1b1b2-

科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
一个与球心距离为1的平面截球体所得的圆面面积为π,则球的体积为( )
A.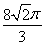 B.
B.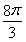 C.
C.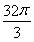 D.8π
D.8π
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷2练习卷(解析版) 题型:选择题
在梯形ABCD中,AB∥CD,且|AB|=λ|DC|,设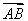 =a,
=a,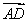 =b,则
=b,则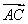 =( )
=( )
A.λa+b B.a+λb
C.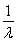 a+b D.a+
a+b D.a+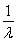 b
b
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
设z=x+y,其中实数x,y满足 若z的最大值为6,则z的最小值为( )
若z的最大值为6,则z的最小值为( )
A.-3 B.-2
C.-1 D.0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练D组练习卷(解析版) 题型:解答题
已知函数f(x)=aln x=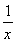 (a为常数).
(a为常数).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,求a的值;
(2)求函数f(x)的单调区间;
(3)当x≥1时,f(x)≤2x-3恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(解析版) 题型:解答题
已知向量m=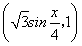 ,n=
,n=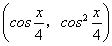 .
.
(1)若m·n=1,求cos 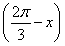 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练A组练习卷(解析版) 题型:解答题
已知函数f(x)=x2+2ax+1(a∈R),f′(x)是f(x)的导函数.
(1)若x∈[-2,-1],不等式f(x)≤f′(x)恒成立,求a的取值范围;
(2)解关于x的方程f(x)=|f′(x)|; ?
(3)设函数g(x)=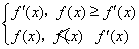 ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练F组练习卷(解析版) 题型:填空题
为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的得分,用茎叶图表示如图所示,则该组数据的方差为________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练C组练习卷(解析版) 题型:填空题
设变量x,y满足不等式组 ,则目标函数z=2x+3y的最小值是________.
,则目标函数z=2x+3y的最小值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com