
【题目】已知△ABC的三个顶点A(4,﹣6),B(﹣4,0),C(﹣1,4),求:
(1)BC边的垂直平分线EF的方程;
(2)AB边的中线的方程.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知f(x)=![]() ,x∈[1,+∞).
,x∈[1,+∞).
(1)当a=![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)= ![]() +lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣
+lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣ ![]() ﹣lnx(m∈R).
﹣lnx(m∈R).
(Ⅰ)求θ的值;
(Ⅱ)若f(x)﹣g(x)在[1,+∞)上为单调函数,求m的取值范围;
(Ⅲ)设h(x)= ![]() ,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,acosC+ ![]() asinC﹣b﹣c=0.
asinC﹣b﹣c=0.
(1)求角A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)= ![]() (万元).当年产量不小于80千件时,C(x)=51x+
(万元).当年产量不小于80千件时,C(x)=51x+ ![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( ) 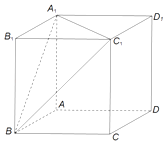
A.2π
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水果树的产量![]() (单位:百千克)与肥料费用(单位:百元)满足如下关系:
(单位:百千克)与肥料费用(单位:百元)满足如下关系:  .此外,还需要投入其它成本(如施肥的人工费等)
.此外,还需要投入其它成本(如施肥的人工费等)![]() 百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为
百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求![]() 的函数关系式;
的函数关系式;
当投入的肥料费用为多少时,该水果树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一组合几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD且PD=AD=2EC=2.
(I)求证:AC⊥平面PDB;
(II)求四棱锥B﹣CEPD的体积;
(III)求该组合体的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com