解:方法一:设公差为d,若d≥0,则an=a1+(n-1)d>0,
∴Sn关于n单调递增,与S7=S13矛盾,故d<0.
又Sn=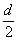 n2+a1-
n2+a1-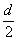 n,
n,
∴点(n,Sn)在开口朝下的抛物线上.
∴n=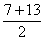 =10时,Sn最大.
=10时,Sn最大.
方法二:由S7=S13知a8+a9+…+a12+a13=0,
∴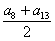 ×6=0,
×6=0,
∴a10+a11=a8+a13=0.
设公差为d,
若d≥0,由a1>0,知a10>0,a11>0,与a10+a11=0矛盾,
∴d<0.
∴a10>a11.又a10+a11=0,
∴a10>0,a11<0.
∴S10最大,即n=10时,Sn最大.
