
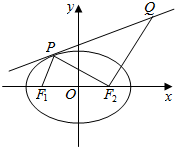
 已知F1,F2是椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$,P(x0,y0)是Γ上异于左右顶点的任意一点,且△PF1F2的面积的最大值为1.
已知F1,F2是椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$,P(x0,y0)是Γ上异于左右顶点的任意一点,且△PF1F2的面积的最大值为1.分析 (Ⅰ)通过判断PF1F2的面积最大时的位置列出方程组,即可求出ab,得到椭圆的方程.
(Ⅱ)利用椭圆的对称性,判断点Q所在的定直线与x轴垂直,猜想直线m:x=2.设直线l:y-y0=k(x-x0)与椭圆联立,消去y,利用相切,△=0,求出k,得到直线l:$y=-\frac{x_0}{{2{y_0}}}(x-{x_0})+{y_0}$,直线$Q{F_2}:\frac{y}{x-1}=-\frac{{{x_0}-1}}{y_0}$,消去y,利用分析法证明即可.
解答 解:(Ⅰ)依题意可知当P在短轴端点时,△PF1F2的面积最大,
可得$\left\{\begin{array}{l}\frac{1}{2}×2c×b=1\\ \frac{c}{a}=\frac{{\sqrt{2}}}{2}\end{array}\right.⇒\left\{\begin{array}{l}{a^2}=2\\{b^2}=1\end{array}\right.$,
所以椭圆$Γ:\frac{x^2}{2}+{y^2}=1$----------------(4分)
(Ⅱ)根据椭圆的对称性可知,点Q所在的定直线与x轴垂直
令P为短轴端点,则PQ:y=1,直线QF2:y=x-1,此时Q(2,0),猜想直线m:x=2---(6分)
设直线l:y-y0=k(x-x0)与椭圆$Γ:\frac{x^2}{2}+{y^2}=1$联立得:${x^2}+2{[kx+({y_0}-k{x_0})]^2}=2$$(1+2{k^2}){x^2}+4k({y_0}-k{x_0})x+2{({y_0}-k{x_0})^2}-2=0$$△=16{k^2}{({y_0}-k{x_0})^2}-4(1+2{k^2})(2{({y_0}-k{x_0})^2}-2)=0$$△=-4(2{({y_0}-k{x_0})^2}-2-4{k^2})=0$,即${({y_0}-k{x_0})^2}-1-2{k^2}=0$,$({x_0}^2-2){k^2}-2{x_0}{y_0}•k+{y_0}^2-1=0$,$-2{y_0}^2{k^2}-2{x_0}{y_0}•k-\frac{{{x_0}^2}}{2}=0$,解得${y_0}^2{k^2}+{x_0}{y_0}•k+\frac{{{x_0}^2}}{4}=0$,所以${({y_0}k+\frac{x_0}{2})^2}=0$,
所以$k=-\frac{x_0}{{2{y_0}}}$,所以直线l:$y=-\frac{x_0}{{2{y_0}}}(x-{x_0})+{y_0}$------------------------(10分)
直线$Q{F_2}:\frac{y}{x-1}=-\frac{{{x_0}-1}}{y_0}$
消去y得:$\frac{{-\frac{x_0}{{2{y_0}}}(x-{x_0})+{y_0}}}{x-1}=-\frac{{{x_0}-1}}{y_0}$,
要证:x=2,只需证:$Q{F_2}:\frac{{-\frac{x_0}{{2{y_0}}}(2-{x_0})+{y_0}}}{2-1}=-\frac{{{x_0}-1}}{y_0}$成立-------(12分)
即证:$-\frac{x_0}{{2{y_0}}}(2-{x_0})+{y_0}=-\frac{{{x_0}-1}}{y_0}$
即证:$-{x_0}(2-{x_0})+2{y_0}^2=-2({x_0}-1)$
即证:${x_0}^2+2{y_0}^2=2$显然成立
所以原命题得证.---------------------------------------------------------------(14分)
点评 本题考查椭圆方程的求法,直线与椭圆位置关系的综合应用,考查归纳推理以及分析法的综合应用,转化思想的应用,难度比较大.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | 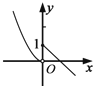 | B. | 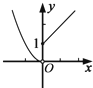 | C. | 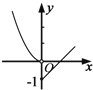 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
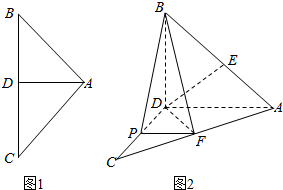 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
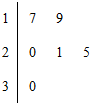 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 | A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com