在平面直角坐标系xy中,O是坐标原点,设函数f(x)=k(x-2)+3的图象为直线l,且l与x轴、y轴分别交于A、B两点,给出下列四个命题:
①使△AOB的面积s=6的直线l仅有一条;
②使△AOB的面积s=8的直线l仅有两条;
③使△AOB的面积s=12的直线l仅有三条;
④使△AOB的面积s=20的直线l仅有四条.
其中所有真命题的序号是________.
②③④
分析:由已知得出三角形的面积公式,由s的值分别解出k的值即可.
解答:由已知条件:函数f(x)=k(x-2)+3的图象为直线l,且l与x轴、y轴分别交于A、B两点,作出图形:
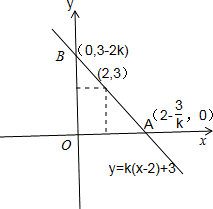
可知k≠0.
由图可知:S
△OAB=
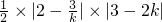
=
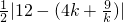
.
①当s=6时,则
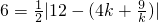
,解得
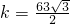
,故符合条件的直线l有两条,故①不正确;
②当s=8时,由8=
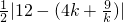
,解得
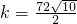
,故符合条件的直线l有两条,故②正确;
③当s=12时,由12=
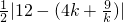
,解得
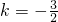
,
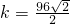
,故符合条件的直线仅有3条,故③正确;
④当s=20时,由20=
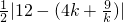
,解的
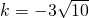
,k=
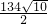
,故符合条件的直线l共有四条,故④正确.
综上可知:正确的命题为②③④.
故答案为②③④.
点评:利用分类讨论的思想是解题的关键.

 学习实践园地系列答案
学习实践园地系列答案