Question

已知函数f(x)=的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.

(1)求函数y=f(x)的解析式;

(2)求函数y=f(x)的单调区间.

Answer 1

剖析:(1)f′(1)即为x+2y+5=0的斜率,从而得出一个关于a、b的关系式.点M(-1,f(-1))在切线上,又得出一个关于a、b的等量关系式.从而可求出a、b.

    (2)利用导数可求y=f(x)的单调区间.

解:(1)由函数f(x)的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0,知

    -1+2f(-1)+5=0,即f(-1)=-2,f′(-1)=-.

    ∵f′(x)=,

    ∴

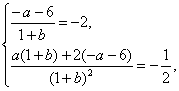
    即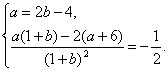

    解得a=2,b=3(∵b+1≠0,b=-1舍去).

    ∴所求的函数解析式是f(x)=.

    (2)f′(x)=.

    令-2x²+12x+6=0,解得x₁=3-2,x₂=3+2.

    当x＜3-2或x＞3+2时,f′(x)＜0;

    当3-2＜x＜3+2时,f′(x)＞0.

    所以f(x)=在(-∞,3-2)内是减函数,在(3-2,3+2)内是增函数,在(3+2,+∞)内是减函数.

讲评:本题主要考查函数的单调性、导数的应用等知识,考查运用数学知识分析问题和解决问题的能力.