
【题目】设定义在R上的函数f(x)满足f(x+2)=-f(x),且  ,则函数g(x)=lg x的图象与函数f(x)的图象的交点个数为( )
,则函数g(x)=lg x的图象与函数f(x)的图象的交点个数为( )
A.3
B.5
C.9
D.10
【答案】C
【解析】因为函数f(x)满足f(x+2)=-f(x),所以f(x+4)=-f(x+2)=f(x),所以函数f(x)是以4为周期的周期函数,所以在同一平面直角坐标系内作出函数f(x)的图象与函数g(x)=lg x的图象如图所示,由图可知两曲线有9个交点.
所以答案是:C.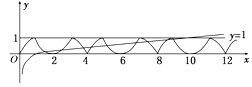
【考点精析】根据题目的已知条件,利用函数的零点与方程根的关系的相关知识可以得到问题的答案,需要掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设集合U={1,2,…,100},TU.对数列{an}(n∈N*),规定:
①若T=,则ST=0;
②若T={n1 , n2 , …,nk},则ST=a ![]() +a
+a ![]() +…+a
+…+a ![]() .
.
例如:当an=2n,T={1,3,5}时,ST=a1+a3+a5=2+6+10=18.
已知等比数列{an}(n∈N*),a1=1,且当T={2,3}时,ST=12,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】所谓正三棱锥,指的是底面为正三角形,顶点在底面上的射影为底面三角形中心的三棱锥,在正三棱锥 ![]() 中,
中, ![]() 是
是 ![]() 的中点,且
的中点,且 ![]() ,底面边长
,底面边长 ![]() ,则正三棱锥
,则正三棱锥 ![]() 的体积为 , 其外接球的表面积为 .
的体积为 , 其外接球的表面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 经过
经过 ![]() 为坐标原点,线段
为坐标原点,线段 ![]() 的中点在圆
的中点在圆 ![]() 上.
上.
(1)求 ![]() 的方程;
的方程;
(2)直线 ![]() 不过曲线
不过曲线 ![]() 的右焦点
的右焦点 ![]() ,与
,与 ![]() 交于
交于 ![]() 两点,且
两点,且 ![]() 与圆
与圆 ![]() 相切,切点在第一象限,
相切,切点在第一象限, ![]() 的周长是否为定值?并说明理由.
的周长是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3 ![]() (其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2 m/s,则其耗氧量至少要多少个单位?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,岛 ![]() 、
、 ![]() 相距
相距 ![]() 海里.上午9点整有一客轮在岛
海里.上午9点整有一客轮在岛 ![]() 的北偏西
的北偏西 ![]() 且距岛
且距岛 ![]()
![]() 海里的
海里的 ![]() 处,沿直线方向匀速开往岛
处,沿直线方向匀速开往岛 ![]() ,在岛
,在岛 ![]() 停留
停留 ![]() 分钟后前往
分钟后前往 ![]() 市.上午
市.上午 ![]() 测得客轮位于岛
测得客轮位于岛 ![]() 的北偏西
的北偏西 ![]() 且距岛
且距岛 ![]()
![]() 海里的
海里的 ![]() 处,此时小张从岛
处,此时小张从岛 ![]() 乘坐速度为
乘坐速度为 ![]() 海里/小时的小艇沿直线方向前往
海里/小时的小艇沿直线方向前往 ![]() 岛换乘客轮去
岛换乘客轮去 ![]() 市.
市.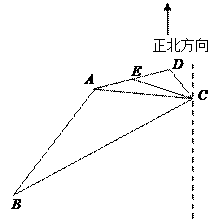
(Ⅰ)若 ![]() ,问小张能否乘上这班客轮?
,问小张能否乘上这班客轮?
(Ⅱ)现测得 ![]() ,
, ![]() .已知速度为
.已知速度为 ![]() 海里/小时(
海里/小时( ![]() )的小艇每小时的总费用为(
)的小艇每小时的总费用为( ![]() )元,若小张由岛
)元,若小张由岛 ![]() 直接乘小艇去
直接乘小艇去 ![]() 市,则至少需要多少费用?
市,则至少需要多少费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com